Measuring overpotential

The three-electrode cell is used to measure the activation overpotential of a cell at various levels of current. Consider the following experiment setup:

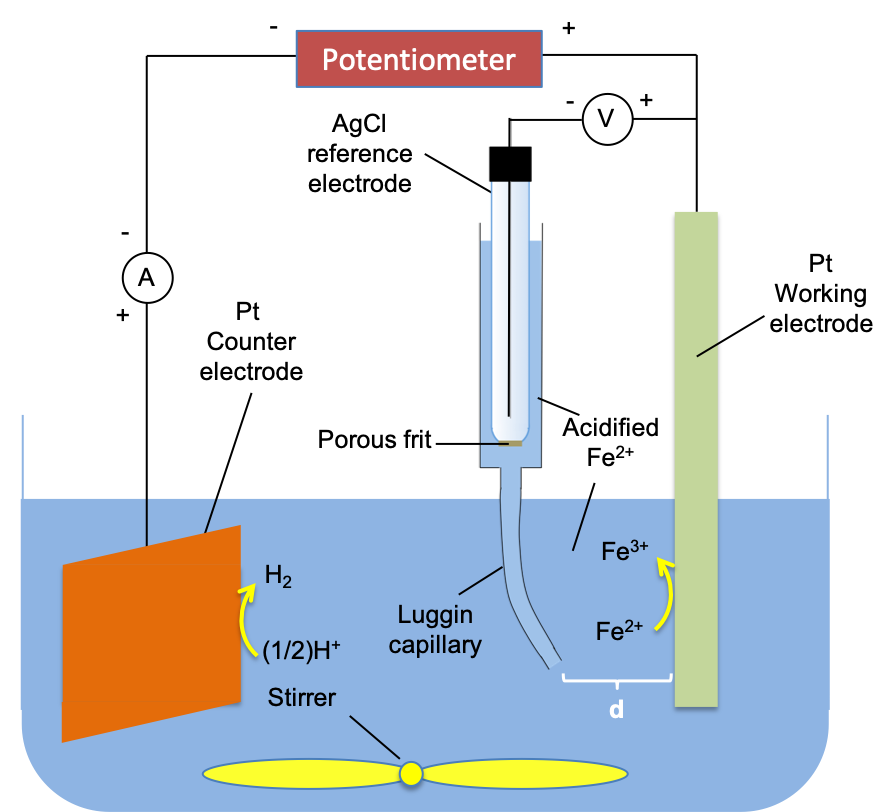
$Fe^{3+}(aq)+e^-\rightleftharpoons Fe^{2+}(aq)\; \; \; \; \; E_{vs\: AgCl(sat'd)}=+0.57\: V$

The opening end of the Luggin capillary is brought very close to the working electrode (d≈0) and the potential of the working electrode E_eqm is measured with the potentiometer and counter electrode removed from the circuit. The two are then reconnected to the circuit and the externally applied potential is turned on to a magnitude greater than 0.57 V (e.g. 0.8V), resulting in Fe²⁺ being oxidised to Fe³⁺ at the anode and H⁺ reduced to H₂ at the cathode. The potential of the working electrode E_pol is again recorded. Assuming that the electrolyte is well-stirred, the difference between E_pol and E_eqm is the activation overpotential of the anode with respect to the current flowing at 0.8 V. By increasing the applied potential, we can tabulate the increasing levels of current, I, flowing in the circuit (see table below) and consequently record the corresponding overpotentials η_act,anodeusing eq61.

If the overpotential at the anode is greater than +100 mV, the second exponential in the Butler-Volmer equation tends to zero, giving:

$j=\frac{I}{A}=j_0\, e^{(1-\alpha)f\eta}\; \; \; \; \; \; \; \; 69$

This means that the net current density at the anode mainly comprises of anodic current density. Taking natural logarithm on both side of eq69,

$ln\left ( \frac{I}{A} \right )=ln j_0+(1-\alpha)f\eta\; \; \; \; \; \; \; \; 70$

Eq70 is known as the Tafel equation, named after the Swiss chemist, Julius Tafel. The plot of ln(I/A) against η is called a Tafel plot and it allows us to find the value of the transfer coefficient $\alpha$ from the gradient of the line and the exchange current density j₀from the intercept. Such an experiment that monitors current at various potentials is called voltammetry.

The three-electrode cell can also be modified slightly to measure the total overpotential of a cell, $\Pi$ . Consider the following experiment with metallic copper for both the anode and cathode, and AgCl electrode as the reference electrode.

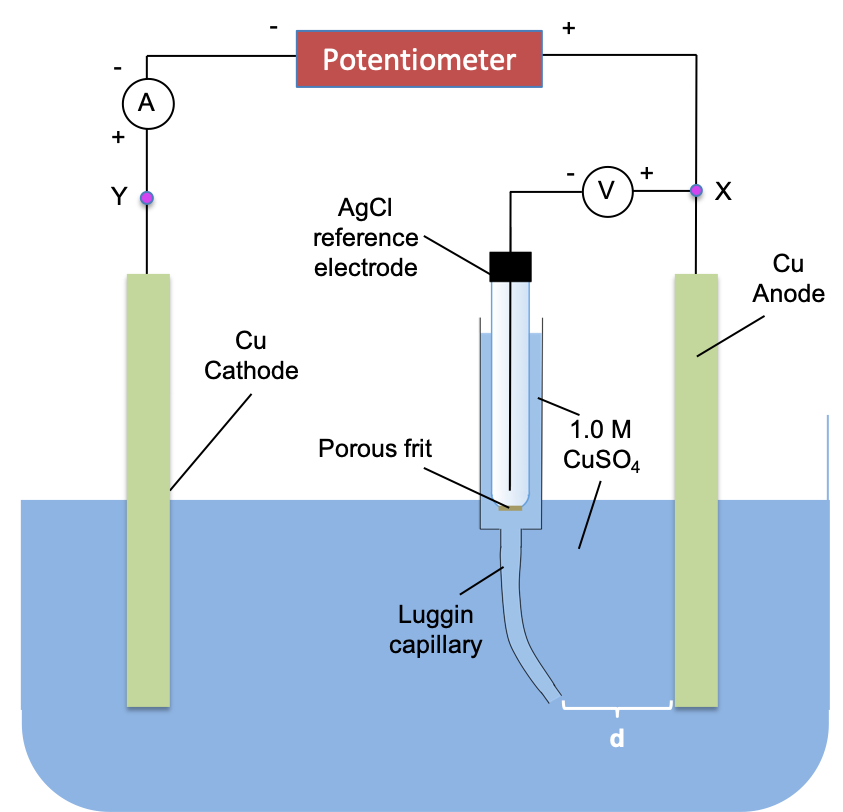
With the potentiometer set to 0 V,

- Measure potential of the left electrode E_{L, eqm} by connecting the reference electrode to junction X.
- Measure potential of the right electrode E_{R, eqm} by connecting the reference electrode to junction Y.

We’d expect E_{L, eqm} = E_{R, eqm}. Next, turn the potentiometer to 1.0 V and

- Measure potential of the left electrode (anode) E_{an, pol} by connecting the reference electrode to junction X.
- Measure potential of the right electrode (cathode) E_{cat, pol} by connecting the reference electrode to junction Y.

We’d expect E_{an, pol} > E_{L, eqm} and E_{cat, pol} < E_{R, eqm}.

$\eta_{an}=E_{an,pol}-E_{L,eqm}>0\; \; \; and\; \; \; \eta_{cat}=E_{cat,pol}-E_{R,eqm}<0$

$\Pi=\eta_{an}+\left | \eta_{cat} \right |$

We can also measure IR drop (in mV/cm) for the above setup by setting the external applied voltage at 1.0 V and measuring the anode potential at different Luggin capillary distances, d.

Measuring overpotential

Next article: Pourbaix diagram

Previous article: Three-electrode cell

Content page of advanced electrochemistry

Content page of Advanced chemistry

Main content page

Leave a Reply Cancel reply