Molecular rotational energies

Molecular rotational energies are quantised states arising from rotation about principal axes, determined by the moments of inertia. These levels are fundamental in molecular spectroscopy.

Diatomic rigid rotor

For a diatomic rigid rotor, the rotational Hamiltonian is given by eq4a, $\hat{H}_{rot}=\frac{\hat{J}^2}{2I}$ . Here, $\hat{J}^2$ is the square of the total angular momentum operator, with the eigenvalues $J(J+1)\hbar^2$ (derived using orbital angular momentum ladder operators), where $J=0,1,2,\cdots$ is the rotational quantum number and $\hbar=\frac{h}{2\pi}$ . Therefore, the rotational energy levels of a diatomic molecule are given by:

$E=J(J+1)\frac{\hbar^2}{2I}\;\;\;\;\;\;\;\;44$

Eq44 can also be expressed in terms of the rotational constant $B=\frac{\hbar}{4\pi cI$ :

$E=hcBJ(J+1)\;\;\;\;\;\;\;\;45$

where $h$ is the Planck constant and $c$ is the speed of light.

However, rotational energies are typically reported as wavenumbers in molecular spectroscopy. Substituting $E=h\nu$ and $c=\nu\lambda$ into eq45 yields $\tilde{\nu}=BJ(J+1)$ , which is a function of $J$ . Therefore,

$F(J)=BJ(J+1)\;\;\;\;\;\;\;\;46$

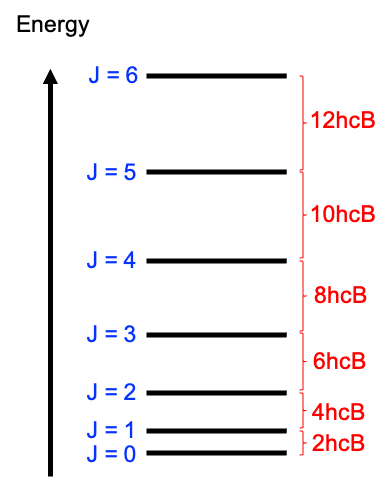
This indicates that the separation between adjacent rotational levels increases linearly with $J$ (see above diagram), as given by:

$F(J)-F(J-1)=2BJ\;\;\;\;\;\;\;\;47$

Furthermore, each energy level (i.e. eq44 for a particular value of $J$ ) is $(2J+1)$ -fold degenerate due to the allowed eigenvalues of the $z$ –component of angular momentum, which are $M_J\hbar$ , where $M_J=-J,-J+1,\cdots,J$ . In the absence of an external magnetic field, these sublevels are degenerate.

Other linear rotors

A rigid linear triatomic molecule (e.g. HCN) behaves similarly as a diatomic rigid rotor when rotating about an axis perpendicular to its bond axis. The moment of inertia about the molecular axis is essentially zero due to the absence of perpendicular mass displacement. Therefore, the rotational energy levels are, per eq44:

$E=J(J+1)\frac{\hbar^2}{2I}\;\;\;\;or\;\;\;\;F(J)=BJ(J+1)$

where $I$ is given by eq15.

Similar to diatomic molecules, each $E$ is $(2J+1)$ -fold degenerate in the absence of an external magnetic field.

Question

Is C₂H₂ also a linear rotor?

Answer

Yes. Its rotational energy levels are also given by eq44 and eq46.

Symmetric rotors

Symmetric rotors have two equal moments of inertia $I_{\perp}$ about mutually orthogonal axes. Each of these is perpendicular to a third rotational axis associated with a distinct, non-zero moment of inertia $I_{\parallel}$ . If $I_{\parallel}< I_{\perp}$ , the molecule is known as a prolate symmetric rotor (shaped like a cigar) and rotates more easily around the principal axis. Examples include NH₃ and CHCl₃. If $I_{\parallel}> I_{\perp}$ , the molecule is called an oblate symmetric rotor (flattened like a disc), and it rotates more easily around an axis perpendicular to the disc. Examples include C₆H₆ and BF₃.

The rotational Hamiltonian of a rigid symmetric rotor in the molecule-fixed frame is given by eq4d:

$\hat{H}_{rot}=\frac{\hat{J}_x^2}{2I_x}+\frac{\hat{J}_y^2}{2I_y}+\frac{\hat{J}_z^2}{2I_z}$

Conventionally, $I_x=I_y=I_z$ and $I_z=I_{\parallel}$ . Furthermore, from eq75, $\hat{J}^2=\hat{J}^2_x+\hat{J}^2_y+\hat{J}^2_z$ . Therefore,

$\hat{H}_{rot}=\frac{\hat{J}_x^2+\hat{J}_y^2}{2I_{\perp}}+\frac{\hat{J}_z^2}{2I_{\parallel}}=\frac{\hat{J}^2}{2I_{\perp}}+\hat{J}^2_z\biggr$\frac{1}{2I_{\parallel}}-\frac{1}{2I_{\perp}}\biggr$\;\;\;\;\;\;\;\;48$

With reference to eq132, and replacing the notations $\hat{L}_z$ , $l$ and $m_l$ with $\hat{J}_z$ , $J$ and $K$ , where $K=-J,-J+1,-J+2,\cdots,J$ , we have $\hat{J}^2_z\psi=\hat{J}_z(\hat{J}_z\psi)=K^2\hbar^2\psi$ . It follows that the rotational energy levels of a rigid symmetric rotor are given by:

$E=J(J+1)\frac{\hbar^2}{2I_{\perp}}+K^2\hbar^2\biggr$\frac{1}{2I_{\parallel}}-\frac{1}{2I_{\perp}}\biggr$\;\;\;\;\;\;\;\;49$

Question

Is $K$ a quantum number? Is it the same as $m_l$ ?

Answer

In eq48, $\hat{J}_z$ refers to the component of the angular momentum operator along the symmetry axis (or $z$ -axis) in the molecule-fixed frame, not the $z$ -axis in the laboratory frame. Although its eigenvalues have the same form as those of $\hat{J}_z$ in the laboratory frame, it is a different quantum number from $m_l$ (or $M_J$ ). An analogy can be made with the projections of the spin vector of a spinning top: its projection along its own axis differs in general from the projection along an arbitrary laboratory axis, unless the axes are aligned. While both projections can take similar ranges of values (assuming these values are quantised), they are not equal in general. Likewise, $K$ and $M_J$ are related to projections in different frames and are different quantum numbers.

Substituting $\tilde{A}=\frac{\hbar}{4\pi cI_{\parallel}$ and $\tilde{B}=\frac{\hbar}{4\pi cI_{\perp}$ into eq49 yields:

$E=hc\tilde{B}J(J+1)+K^2hc(\tilde{A}-\tilde{B})\;\;\;\;\;\;\;\;50$

Substituting $E=h\nu$ and $c=\nu\lambda$ into eq50 gives $\tilde{\nu}=\tilde{B}J(J+1)+K^2(\tilde{A}-\tilde{B})$ , which is a function of two rotational quantum numbers $J$ and $K$ . Therefore,

$F(J,K)=\tilde{B}J(J+1)+K^2(\tilde{A}-\tilde{B})\;\;\;\;\;\;\;\;51$

When $K=0$ , there is only one distinct moment of inertia, with eq51 reducing to eq46, where $\tilde{B}=B$ . In this case, each $E$ is $(2J+1)$ -fold degenerate in the absence of an external magnetic field. If $K\neq 0$ , $E$ is determined by the magnitudes of $J$ and $K^2$ . Since $E$ is the same for $(+K)^2$ and $(-K)^2$ for each $J$ in eq49, the energy levels for $+K$ and $-K$ are degenerate. Additionally, there are $2J+1$ possible $M_J$ substates for each value of $J$ . Therefore, the total degeneracy when $K\neq 0$ is $2(2J+1)$ in the absence of an external magnetic field.

Spherical rotors

A spherical rotor has three equal moments of inertia $I_x=I_y=I_z=I$ about three mutually orthogonal axes. It belongs to a point group that is a parent group of that of a symmetric rotor. Therefore, the rotational energy levels of a spherical rotor can be described by eq49 with $I_{\parallel}=I_{\perp}$ , which is equivalent the condition $\tilde{A}=\tilde{B}$ in eq50. This implies that $E$ remains a function of both $J$ and $K$ , and that for a given energy level, $K$ is not restricted to just two values (as in the case of a symmetric rotor), but can take on $2J+1$ different values. It follows that each energy level is $(2J+1)^2$ -fold degenerate in the absence of an external magnetic field.

Molecular rotational energies

Question

Answer

Question

Answer

Next article: Effect of nuclear statistics on rotational states

Previous article: Moments of inertia of spherical rotors

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply