The moments of inertia of a trigonal pyramidal prolate rotor with 
symmetry (e.g. NH3) are characterised by a unique moment of inertia 
around the 
rotational axis (
-axis) and two equal moments of inertia 
perpendicular to the axis, where 
. They are derived using simple geometric considerations.
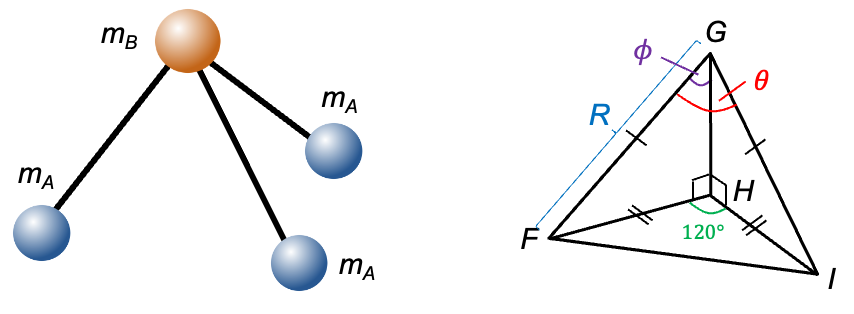
The structure on the right of the above diagram illustrates the geometry of the central atom B (with mass 
) and two of the three A atoms, each with mass 
. Let 
be the angle between an A-B-A bond (between FG and GI), 
be the angle between a B-A bond and the -axis (GH) and 
be the length of each B-A bond. According to the VSEPR theory, 
.
Applying the cosine rule on 
gives ^2=(FG)^2+(GI)^2-2(FG)(GI)cos\theta)
. Since 
, we have
}\;\;\;\;\;\;\;\;20)
Using the cosine rule again on 
and noting that 
yields ^2=3(FH)^2)
. Substituting eq20 into this equation results in
}\;\;\;\;\;\;\;\;21)
Hence, the moment of inertia for symmetric rotors like NH3 along the -axis is:
^2=2m_A(1-cos\theta)R^2\;\;\;\;\;\;\;\;22)
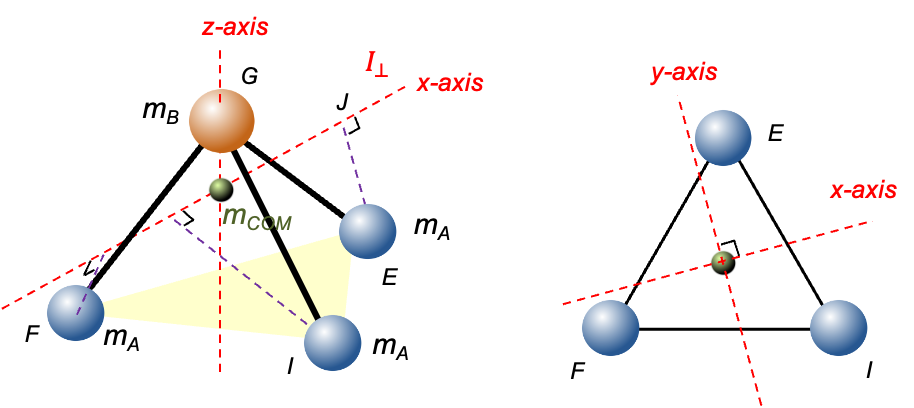
To derive , we begin by noting that the centre of mass of the molecule (green sphere) lies along the -axis (one of three principal axes of rotation), between atom B and the plane formed by the three A atoms (see diagram below). The 
-axis and 
-axis are orthogonal to the -axis and to each other. They intersect at the centre of mass but do not intersect any of the B-A bonds.
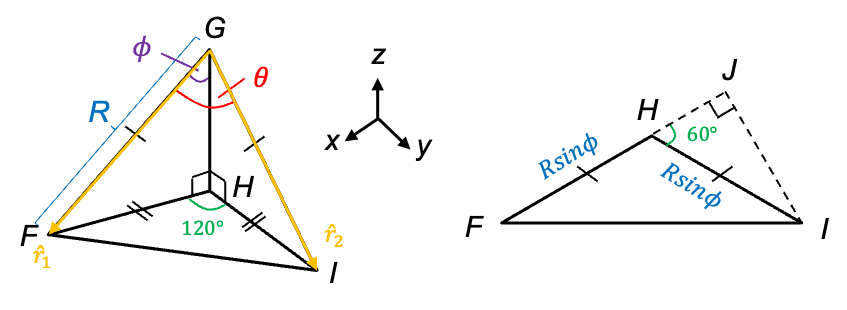
The relationship between the angles and is established by letting atom B be the origin )
and the three A atoms at angles 0°, 120°, 240° around the -axis. Furthermore, let )
be the unit vector pointing from atom B to atom A at F, and )
be the unit vector pointing from atom B to atom A at I (see diagram below).
The dot product of the two vectors is given by 
or 
, which is equivalent to
\;\;\;\;\;\;\;\;23)
Importantly, eq23 is independent of the choice of origin or reference frame even though it was derived with atom B as the origin.
Now, let’s place the origin at the centre of mass of the molecule. The -coordinates of atom B and each of the A atoms are 
and 
respectively. Then, the centre of mass of the molecule satisfies =0)
or
with 
or
Since the position of the centre of mass relative to that of atom B only involves a shift in the -direction, the and coordinates of the three A atoms are those defined by the unit vectors above multiplied by the factor . Therefore, the positions of the atoms are:
|
Atom
|
Coordinates |
|
B
|
) |
|
A (point F)
|
) |
|
A (point I)
|
) |
| A (point E) |
|
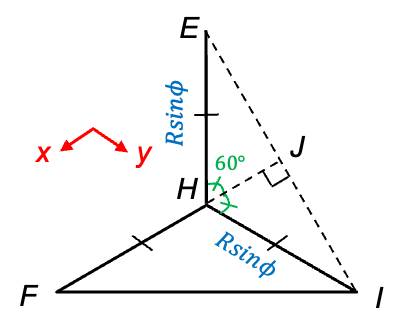
Question
Derive the and coordinates of atom A at point E.
Answer
With reference to the diagram below, we have )
.
Since )
, the moment of inertia of the molecule about the -axis is:
\;\;\;\;\;\;\;\;26)
Substituting the data from the above table into eq26 and simplifying gives:
\;\;\;\;\;\;\;\;27)
Substituting eq23 into eq27 and simplifying yields:
}{3m_A+m_B}+(1-cos\theta)\biggr\]\;\;\;\;\;\;\;\;28)
You’ll find that substituting the data in the above table into the moment of inertia of the molecule about the -axis )
results in the same expression as eq28. Therefore, eq22 and eq28 are the two distinct moments of inertia of a trigonal pyramidal prolate rotor with symmetry.