The photoelectric effect is the ejection of electrons from the surface of a material when light strikes it. This occurs due to the transfer of energy from light to the electrons, providing them with sufficient kinetic energy to be ejected from the material. Heinrich Hertz was the first scientist to discover the photoelectric effect in 1887. Since then, other scientists conducted various experiments to study the effect using apparatus similar to the one in the diagram below:
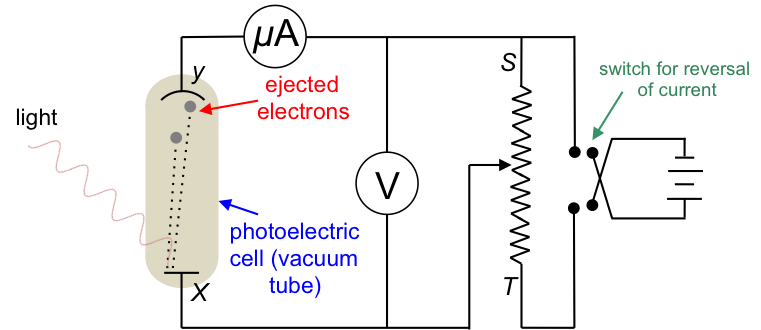
The experiment
The apparatus consists of a photoelectric cell connected to a potentiometer and a battery with a commutator (switch for reversal of current). At the start of the experiment, the potential difference across X and Y is set to zero, i.e. the battery is disconnected from the circuit and the wiper is slid to S. Light of a particular frequency and intensity striking X ejects electrons with different kinetic energies into the vacuum between X and Y, and leaves behind positive charges (holes) at X. The ejected electrons with the proper trajectory reach Y and return along the wire to X, thereby completing the circuit and generating a very small current in the order of a few micro amperes.

Question
Why doesn’t the positively charged holes attract the ejected electrons back to X? Why do the ejected electrons have different kinetic energies?
Answer
Energy has been transferred from the incident radiation to the electrons to overcome the electrostatic forces of attraction. Any electron that leaves X will reach Y if they are ejected at the appropriate angle and not repelled by other electrons in the vacuum tube.
The ejected electrons have different kinetic energies because they reside at different depths of the material’s surface at X prior to ejection. The deeper they are, the lower their kinetic energies upon ejection due to electrostatic (nuclear forces of attraction) and mechanical factors (collisions).
The next stage of the experiment involves connecting the battery to the circuit with its positive terminal to Y and negative terminal to X. The wiper is gradually slid towards T and the current in the circuit increases and reaches a saturation value.
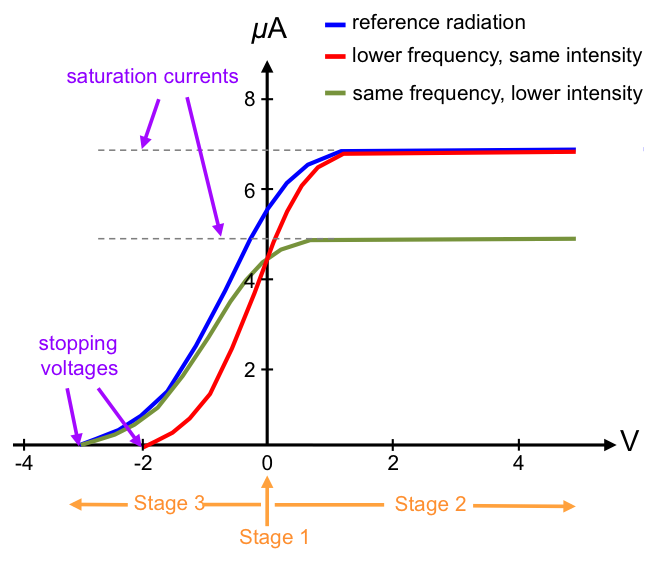
In the last stage of the experiment, the terminals of the battery are connected to the circuit in reverse and the wiper is returned closer to S. X is now positively charged and fewer electrons reach Y, causing the current in the circuit to decrease. As the wiper is again slid towards T, the potential difference across XY increases (the voltmeter reading becomes more negative) and the current decreases further until it drops to zero. The voltage required to completely stop the current from flowing in the circuit is called the stopping voltage. The experiment is then repeated by separately varying the frequency of the incident radiation and the intensity of the radiation.
The RESULTS
When incident radiation above a certain threshold frequency impinges the material (electrode) at X,
-
- the current produced is proportional to the intensity (brightness) of the incident radiation but independent of its frequency.
- the absolute value of the stopping voltage is proportional to the frequency of the incident radiation but independent of its intensity.
- the effect is instantaneous, i.e. no time delay between the incidence of light and emission of electrons.
Scientists at that time failed to explain all the results using the wave theory of light, which predicted the following:
- The current produced is proportional to the frequency of the incident radiation. This is because wave theory suggests that the oscillating electric field of the incident light causes electrons to oscillate and eventually break free from the material. The higher the frequency of the incident light, the higher the probability of electrons breaking free from the material.
- The absolute value of the stopping voltage should be proportional to light intensity, as wave theory defines light intensity as energy/(area x time). Therefore, a higher energy light source should require a stopping potential of a larger magnitude.
- There should be a time difference between the ejection of electrons at low light intensity versus high light intensity, because incident light energy is shared throughout the cathode and is cumulative according to classical wave theory (i.e. the amplitude of the oscillation of electrons will increase over time as light waves continue to hit the cathode until the electrons have the required energy to be ejected).
EXPLANATION OF RESULTS
In 1905, five years after Max Planck introduced the Planck relation, where the energy of light E is an integer multiple of the product of the Planck constant h and the light’s frequency v, i.e. E = nhv, Albert Einstein proposed that:
Light, in addition to being a wave, is also a particle of a fixed amount of energy of hv, i.e. the incident electromagnetic radiation is quantised.
A particle of light of energy hv is subsequently called a photon.

Explanation for part 1 of the results
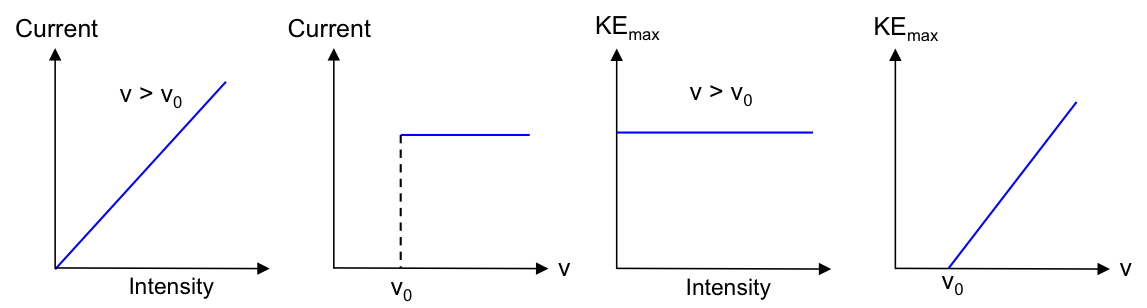
The current produced is proportional to the intensity (brightness) of the incident radiation but independent of its frequency.
If Einstein is correct and light has particle-like behaviour, light intensity can be defined as the rate of photon arrival per unit area. For a fixed value of v, the increase in light intensity is equivalent to the increase in the rate of photon hitting the material at a constant energy of hv per photon. Therefore, when light intensity increases, the amount of ejected electrons reaching Y and flowing in the circuit increases.
For a fixed intensity, increasing the frequency of the incident radiation (i.e., increasing the energy of the incident photons) only increases the kinetic energy of the ejected electrons and not the amount of electrons, as an incident photon, according to Einstein, interacts with an electron by transferring all its energy to the latter (i.e., the energy is not shared by more than one electron). Furthermore, the results are contingent on the incident radiation being above a certain threshold frequency vo. This led Einstein to establish the following equation:
where is the work function, i.e., the energy needed to overcome the attractive forces between the electron and the nuclei in the material, and KEmax is the maximum kinetic energy of an ejected electron (note that an electron residing deeper in the material has KE < KEmax).
The work function is an intrinsic property of the material (a metal or metalloid) and has a value that varies with different elements.

Question
Why does current increase and reach a saturation value in the second stage of the experiment?
Answer
With the battery connected to the circuit and as the wiper is gradually slid towards T, the potential difference between YX increases. The positively charged Y attracts additional electrons, which previously did not have the proper trajectory to reach it, and the current in the circuit increases. As the wiper slides further away from S, a saturation current is produced because the total number of ejected electrons is dependent only on the incident radiation (assuming that the maximum potential difference across YX is not high enough to ionise any electron at X).
Explanation for part 2 of the results
The absolute value of the stopping voltage is proportional to the frequency of the incident radiation but independent of its intensity.
At the last stage of the experiment, the battery is connected with its positive terminal to X. Electrons leaving X are now subjected to a constant opposing electric force (uniform electric field across XY) that decelerates their motion towards Y. If we assume that the fastest electrons leave X with the same KEmax expressed in eq2 (where ), the difference in kinetic energy between these electrons at X and the same electrons at Y, according to the principle of conservation of energy, must be equal to the energy required to establish the opposing potential difference across XY, i.e.
. Since
when no current flows in the circuit, we can expressed the relation between the stopping potential and the maximum kinetic energy of the ejected electrons as:
In other words, the higher the kinetic energy of the ejected electrons, the higher the potential needed to stop the current flow. According to eq2, KEmax for a particular cathode is proportional only to v. Therefore, Vstop is proportional to the frequency of the incident radiation but independent of its intensity.
Graphically, we can express parts 1 and 2 of the results as follows:
Explanation for part 3 of the results
The effect is instantaneous, i.e. no time delay between the incidence of light and emission of electrons.
Finally, let’s consider a light of low intensity impinging on the material at X (i.e. light with energy lower than ). According to the classical wave theory, there would be a time interval between light hitting the material and the emission of an electron. However, current is zero at such an intensity and classical theory fails. Since the emission of electrons does not occur when
, and is instantaneous when
, light energy must be quantised.

Question
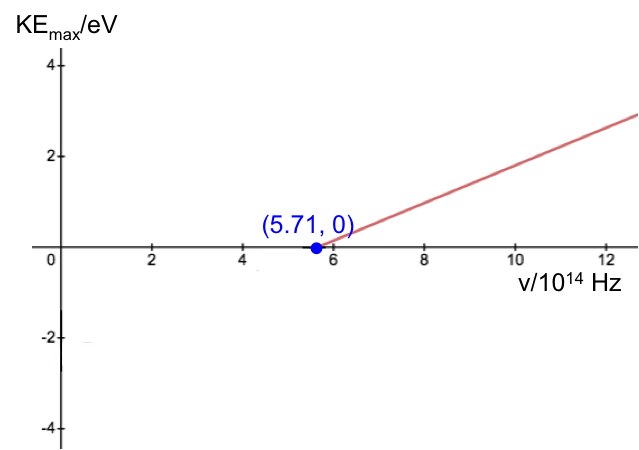
Calculate the Planck constant, the threshold frequency and the work function of sodium using the graph below (1eV = 1.602 x 10-19 J).
Answer
Rearranging eq2,
The value of the work function is given by the vertical intercept, i.e. 2.36 eV.
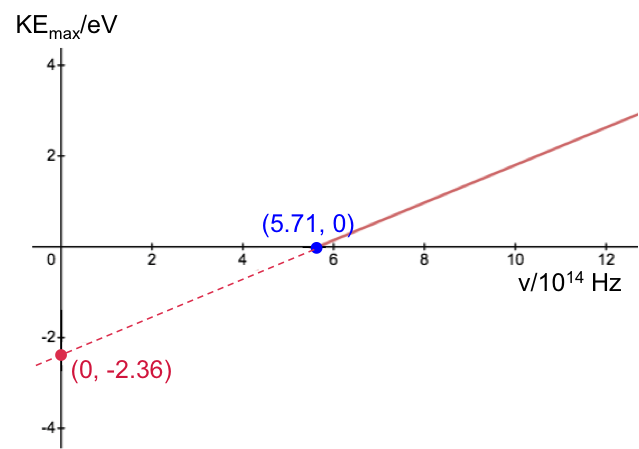
The threshold frequency is the frequency when (the horizontal intercept), i.e. 5.71 x 1014 Hz. The Plank constant is:
