Quantum orbital angular momentum operators (spherical coordinates)

The quantum orbital angular momentum operators in spherical coordinates are derived using the following diagram:

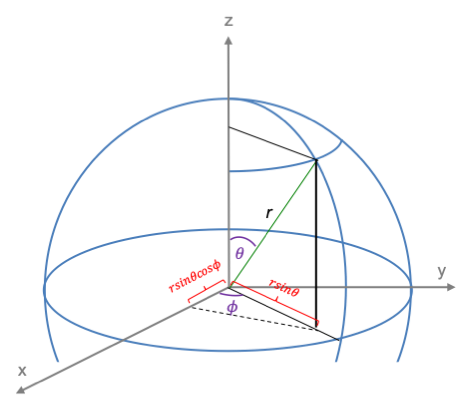
where

$x=rsin\theta cos\phi\; \; \; \; y=rsin\theta sin\phi\; \; \; \; z=rcos\theta\; \; \; \; r=\sqrt{x^{2}+y^{2}+z^{2}}\; \; \; \; \; \; \; \; 77$

Therefore,

$\frac{\partial r}{\partial x}=\frac{\partial \sqrt{x^{2}+y^{2}+z^{2}}}{\partial x}=\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}=\frac{x}{r}=sin\theta cos\phi\; \; \; \; \; \; \; \; 78$

Similarly,

$\frac{\partial r}{\partial y}=sin\theta sin\phi\; \; \; \; \; \; \; \; 79$

$\frac{\partial r}{\partial z}= cos\theta\; \; \; \; \; \; \; \; 80$

Furthermore, by differentiating $cos\theta=\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}$ implicitly with respect to $x$ and separately with respect to $y$ , and rearranging, we have

$\frac{\partial\theta}{\partial x}=\frac{cos\theta cos\phi}{r}\; \; \; \; \; \; \; \; 81$

$\frac{\partial\theta}{\partial y}=\frac{cos\theta sin\phi}{r}\; \; \; \; \; \; \; \; 82$

Question

Show that $sin\phi=\frac{y}{\sqrt{x^{2}+y^{2}}}$ , $cos\phi=\frac{x}{\sqrt{x^{2}+y^{2}}}$ and $sin\theta=\frac{\sqrt{x^{2}+y^{2}}}{\sqrt{x^{2}+y^{2}+z^{2}}}$ .

Answer

To find expressions for $sin\phi$ and $cos\phi$ , we let $\theta=\frac{\pi}{2}$ for the first three equations of eq77, which gives us $x=rcos\phi$ , $y=rsin\phi$ and $z=0$ . So,

$cos\phi=\frac{x}{\sqrt{x^{2}+y^{2}}}\; \; \; \; \; \;sin\phi=\frac{y}{\sqrt{x^{2}+y^{2}}}$

Substituting these two expressions back into either the first or second equation of eq77, we have

$sin\theta=\frac{\sqrt{x^{2}+y^{2}}}{\sqrt{x^{2}+y^{2}+z^{2}}}$

Implicit differentiation of $sin\theta=\frac{\sqrt{x^{2}+y^{2}}}{\sqrt{x^{2}+y^{2}+z^{2}}}$ , $sin\phi=\frac{y}{\sqrt{x^{2}+y^{2}}}$ and $cos\phi=\frac{x}{\sqrt{x^{2}+y^{2}}}$ with respect to $z$ , $x$ and $y$ respectively gives

$\frac{\partial\theta}{\partial z}=-\frac{sin\theta}{r}\; \; \; \; \; \; \; \; 83$

$\frac{\partial\phi}{\partial x}=-\frac{sin\phi}{rsin\theta}\; \; \; \; \; \; \; \; 84$

$\frac{\partial\phi}{\partial y}=\frac{cos\phi}{rsin\theta}\; \; \; \; \; \; \; \; 85$

Since $\phi$ is independent of $z$

$\frac{\partial\phi}{\partial z}=0\; \; \; \; \; \; \; \; 86$

Applying the multivariable chain rule to $f\left ( r,\theta,\phi \right )$ , we have:

$\frac{\partial}{\partial x}=\frac{\partial r}{\partial x}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial x}\frac{\partial}{\partial \phi}\; \; \; \; \; \; \; \; 87$

$\frac{\partial}{\partial y}=\frac{\partial r}{\partial y}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial y}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial y}\frac{\partial}{\partial \phi}\; \; \; \; \; \; \; \; 88$

$\frac{\partial}{\partial z}=\frac{\partial r}{\partial z}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial z}\frac{\partial}{\partial \theta}+\frac{\partial\phi}{\partial z}\frac{\partial}{\partial \phi}\; \; \; \; \; \; \; \; 89$

Substitute i) eq78, eq81 and eq84 in eq87, ii) eq79, eq82 and eq85 in eq88 and iii) eq80, eq83 and eq86 in eq89, we have

$\frac{\partial}{\partial x}=sin\theta cos\phi\frac{\partial}{\partial r}+\frac{cos\theta cos\phi}{r}\frac{\partial}{\partial \theta}-\frac{sin\phi }{rsin\theta}\frac{\partial}{\partial \phi}\; \; \; \; \; \; \; \; \; \; 90$

$\frac{\partial}{\partial y}=sin\theta sin\phi\frac{\partial}{\partial r}+\frac{cos\theta sin\phi}{r}\frac{\partial}{\partial \theta}+\frac{cos\phi }{rsin\theta}\frac{\partial}{\partial \phi}\; \; \; \; \; \; \; \; \; \; 91$

$\frac{\partial}{\partial z}=cos\theta \frac{\partial}{\partial r}-\frac{sin\theta}{r}\frac{\partial}{\partial \theta}\; \; \; \; \; \; \; \; \; \; 92$

respectively.

Substitute eq77, eq90, eq91 and eq92 in eq72, eq73 and eq74, we have

$\hat{L}_x=\frac{\hbar}{i}\left ( -sin\phi\frac{\partial}{\partial \theta}-\frac{cos\theta cos\phi}{sin\theta}\frac{\partial}{\partial \phi}\right )\; \; \; \; \; \; \; \; 93$

$\hat{L}_y=\frac{\hbar}{i}\left (cos\phi\frac{\partial}{\partial \theta}-\frac{cos\theta sin\phi}{sin\theta}\frac{\partial}{\partial \phi}\right )\; \; \; \; \; \; \; \; 94$

$\hat{L}_z=\frac{\hbar}{i}\frac{\partial}{\partial \phi}\; \; \; \; \; \; \; \; 95$

respectively.

Substitute eq93, eq94 and eq95 in eq75, we have, with some algebra

$\hat{L}^{2}=-\hbar^{2}\left ( \frac{\partial^{2}}{\partial \theta^{2}}+\frac{1}{sin^{2}\theta}\frac{\partial^{2}}{\partial \phi^{2}}+\frac{cos\theta}{sin\theta}\frac{\partial}{\partial \theta}\right )$

or equivalently

$\hat{L}^{2}=-\hbar^{2}\left \[ \frac{1}{sin^{2}\theta}\frac{\partial^{2}}{\partial \phi^{2}}+\frac{1}{sin\theta}\frac{\partial}{\partial \theta}\left ( sin\theta\frac{\partial}{\partial \theta}\right )\right ]\; \; \; \; \; \; \; \; 96$

$\hat{L}^{2}$ is the quantum orbital angular momentum operator and each of its eigenvalues is the square of the orbital angular momentum of an electron.

Question

Show that eq76 is $\frac{\hbar}{i}\left ( \boldsymbol{\mathit{\phi}}\frac{\partial}{\partial \theta}- \boldsymbol{\mathit{\theta}}\frac{1}{sin \theta}\frac{\partial}{\partial \phi}\right )$ in spherical coordinates.

Answer

Substitute eq93, eq94, eq95 and unit vectors in spherical coordinates $\boldsymbol{\mathit{i}}= \boldsymbol{\mathit{r}}sin\theta cos\phi+ \boldsymbol{\mathit{\theta}}cos\phi cos\theta-\boldsymbol{\mathit{\phi}}sin\phi$ , $\boldsymbol{\mathit{j}}= \boldsymbol{\mathit{r}}sin\theta sin\phi+ \boldsymbol{\mathit{\theta}}cos\theta sin\phi-\boldsymbol{\mathit{\phi}}cos\phi$ and $\boldsymbol{\mathit{k}}= \boldsymbol{\mathit{r}}cos\theta- \boldsymbol{\mathit{\theta}}sin\theta$ in eq76. we have, after some algebra, we have

$\boldsymbol{\mathit{\hat{L}}}=\frac{\hbar}{i}\left ( \boldsymbol{\mathit{\phi}}\frac{\partial}{\partial\theta}- \boldsymbol{\mathit{\theta}}\frac{1}{sin\theta}\frac{\partial}{\partial\phi}\right )\; \; \; \; \; \; \; \; 97$

Question

Show that $\boldsymbol{\mathit{\hat{L}}}\cdot\boldsymbol{\mathit{\hat{L}}}=\hat{L}^{2}$ .

Answer

Substituting eq97 in $\hat{L}^{2}=\boldsymbol{\mathit{L}}\cdot\boldsymbol{\mathit{L}}$ and using $\frac{\partial\boldsymbol{\mathit{\phi}}}{\partial\theta}=0$ , $\frac{\partial\boldsymbol{\mathit{\theta}}}{\partial\theta}=-\boldsymbol{\mathit{r}}$ , $\frac{\partial\boldsymbol{\mathit{\phi}}}{\partial\phi}=-\boldsymbol{\mathit{r}} sin\theta-\boldsymbol{\mathit{\theta}}cos\theta$ and $\frac{\partial\boldsymbol{\mathit{\theta}}}{\partial\phi}=\boldsymbol{\mathit{\phi}}cos\theta$ , we have

$\hat{L}^{2}=\boldsymbol{\mathit{L}}\cdot\boldsymbol{\mathit{L}}=-\hbar^{2}\left [\frac{\partial^{2}}{\partial\theta^{2}}+\frac{cos\theta}{sin\theta}\frac{\partial}{\partial\theta}+\frac{1}{sin^{2}\theta}\frac{\partial^{2}}{\partial\phi^{2}}\right ]\; \; \; \; \; \; \; \; 98$

Quantum orbital angular momentum operators (spherical coordinates)

Question

Answer

Question

Answer

Question

Answer

Next article: commutation relations of quantum orbital angular momentum operators

Previous article: quantum orbital angular momentum operators (cartesian coordinates)

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply