Commutation relations of quantum orbital angular momentum operators

The three orbital angular momentum component operators do not commute with one another.

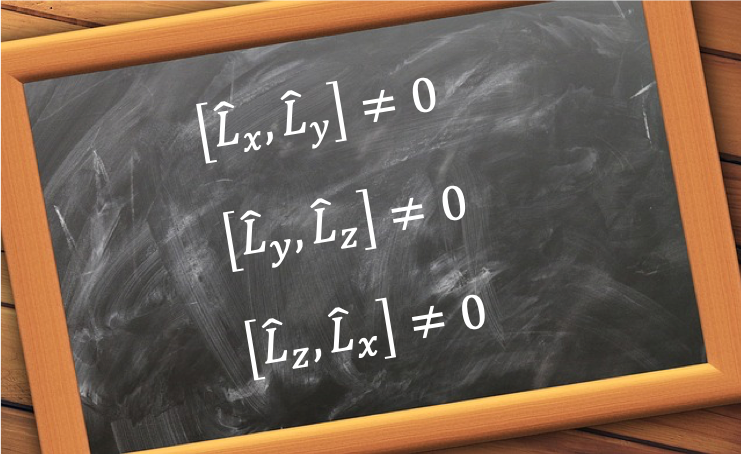
To show that $\left [ \hat{L}_x,\hat{L}_y \right ]\neq 0$ , we substitute eq72 and eq73 in $\left [ \hat{L}_x,\hat{L}_y \right ]$ , giving $\left [ \hat{L}_x,\hat{L}_y \right ]=\hbar^{2}\left [ x\frac{\partial}{\partial y}-y\frac{\partial}{\partial x}\right ]$ , which when substituted with eq74, returns

$\left [ \hat{L}_x,\hat{L}_y \right ]=i\hbar\hat{L}_z\; \; \; \; \; \; \; \; 99$

Repeating the above procedure, we get

$\left [ \hat{L}_y,\hat{L}_z \right ]=i\hbar\hat{L}_x\; \; \; \; \; \; \; \; 100$

$\left [ \hat{L}_z,\hat{L}_x \right ]=i\hbar\hat{L}_y\; \; \; \; \; \; \; \; 101$

Hence, each of the three orbital angular momentum component operators do not commute with the other two. Next, to show that $\hat{L}^{2}$ commutes with all 3 orbital angular momentum component operators, we begin with

$\small \left [ \hat{L}^{2},\hat{L}_x \right ]=\left (\hat{L}_x^{\; 2}+\hat{L}_y^{\; 2}+\hat{L}_z^{\; 2}\right )\hat{L}_x-\hat{L}_x\left (\hat{L}_x^{\; 2}+\hat{L}_y^{\; 2}+\hat{L}_z^{\; 2}\right )=\left [ \hat{L}_y^{\; 2},\hat{L}_x \right ]+\left [ \hat{L}_z^{\; 2},\hat{L}_x \right ]$

Using the identity $\small \left [ \hat{L}_a^{\; 2},\hat{L}_b \right ]=\hat{L}_a\left [ \hat{L}_a,\hat{L}_b \right ]+\left [ \hat{L}_a,\hat{L}_b \right ]\hat{L}_a$ ,

$\small \left [ \hat{L}^{2},\hat{L}_x \right ]=\hat{L}_y\left [ \hat{L}_y,\hat{L}_x \right ]+\left [ \hat{L}_y,\hat{L}_x \right ]\hat{L}_y +\hat{L}_z\left [ \hat{L}_z,\hat{L}_x \right ]+\left [ \hat{L}_z,\hat{L}_x \right ]\hat{L}_z$

Substitute eq99 and eq101 in the above equation, noting that $\small \left [ \hat{L}_a,\hat{L}_b \right ]=-\left [ \hat{L}_b,\hat{L}_a \right ]$ , we have $\small \left [ \hat{L}^{2},\hat{L}_x \right ]=0$ . Repeating the steps for $\small \left [ \hat{L}^{2},\hat{L}_y \right ]$ and $\small \left [ \hat{L}^{2},\hat{L}_z \right ]$ gives

$\small \left [ \hat{L}^{2},\hat{L}_x \right ]=0\; \; \; \;\left [ \hat{L}^{2},\hat{L}_y \right ]=0\; \; \; \;\left [ \hat{L}^{2},\hat{L}_z \right ]=0\; \; \; \; \; \; \; \; 102$

As mentioned in an earlier article, a common complete set of eigenfunctions can be selected for two operators only if they commute. Therefore, $\small \hat{L}^{2}$ shares a common set of eigenfunctions with each of $\small \hat{L}_x$ , $\small \hat{L}_y$ and $\small \hat{L}_z$ , but we cannot select a common set of eigenfunctions for any pair of angular momentum component operators.

Question

Show that each of the three orbital angular momentum component operators commute with $\small p^{2}$ , $\small \hat{p}^{2}$ , $\small r$ , $\small r^{2}$ and $\small \frac{1}{r}$ , where $\small p^{2}=p_x^{\; 2}+p_y^{\; 2}+p_z^{\; 2}$ and $\small r^{2}=x^{\; 2}+y^{\; 2}+z^{\; 2}$ .

Answer

Substituting eq74 in $\small \left [ \hat{L}_z,x \right ]$ , $\small \left [ \hat{L}_z,y \right ]$ , $\small \left [ \hat{L}_z,z \right ]$ , $\small \left [ \hat{L}_z,p_x \right ]$ , $\small \left [ \hat{L}_z,p_y \right ]$ and $\small \left [ \hat{L}_z,p_z \right ]$ (noting that $\small p_i=m\frac{i}{t}$ , where $\small i=x,y,z$ ) and carrying out the derivatives, we have

$\small \left [ \hat{L}_z,x \right ]=i\hbar y\; \; \; \; \;\left [ \hat{L}_z,y \right ]=-i\hbar x\; \; \; \; \;\left [ \hat{L}_z,z \right ]=0$

$\small \left [ \hat{L}_z,p_x \right ]=i\hbar p_y\; \; \; \; \;\left [ \hat{L}_z,p_y \right ]=-i\hbar p_x\; \; \; \; \;\left [ \hat{L}_z,p_z \right ]=0$

Using the identities $\small \left [ \hat{A},\hat{B}+\hat{C}+\hat{D} \right ]=\left [ \hat{A},\hat{B} \right ]+\left [ \hat{A},\hat{C} \right ]+\left [ \hat{A},\hat{D} \right ]$ and $\small \left [ \hat{A},\hat{B}\hat{C} \right ]=\left [ \hat{A}\hat{B} \right ]\hat{C}+\hat{B}\left[\hat{A},\hat{C} \right ]$ ,

$\small \left [ \hat{L}_z,r^{2} \right ]=\left [ \hat{L}_z,x^{2}+y^{2}+z^{2}\right ]=0$

$\small \left [ \hat{L}_z,r \right ]=\left [ \hat{L}_z,\sqrt{x^{2}+y^{2}+z^{2}}\right ]=0$

$\small \left [ \hat{L}_z,\frac{1}{r} \right ]=\left [ \hat{L}_z,\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right ]=0$

$\small \left [ \hat{L}_z,p^{2} \right ]=\left [ \hat{L}_z,p_x^{\; 2}+p_y^{\; 2}+p_z^{\; 2}\right ]=0\; \; \; \; \; \; \; \; 103$

$\small \left [ \hat{L}_z,\hat{p}^{2} \right ]=0$ can be inferred from eq103. Repeating the same logic for $\small \hat{L}_x$ and $\small \hat{L}_y$ . we have

$\small \left [ \hat{L}_i,r^{2} \right ]=0\; \; \; \;\left [ \hat{L}_i,r \right ]=0\; \; \; \;\left [ \hat{L}_i,\frac{1}{r} \right ]=0\; \; \; \;\left [ \hat{L}_i,p^{2} \right ]=0\; \; \; \;\left [ \hat{L}_i,\hat{p}^{2}\right ]=0\; \; \; \; \; \; \; \; 104$

The commutation relations in the above Q&A are applicable to hydrogenic systems. For a system of 2-electrons, there are cross terms like:

$\small \left [ \hat{L}_{1z},\frac{1}{r_2} \right ]=\left [ \hat{L}_{1z},\frac{1}{\sqrt{x_2^{\; 2}+y_2^{\; 2}+z_2^{\; 2}}} \right ]=0\; \; \; \; \; \; \; \; 105$

which are useful in determining the commutation relations between $\small \hat{L}^{2}$ and the multi-electron Hamiltonian, for example $\small \left [ \hat{L}_{1z}+\hat{L}_{2z},\frac{1}{r_1}+\frac{1}{r_2} \right ]=0$ .

Question

Show that $\small \left [ \hat{L}^{2},\hat{p}^{2} \right ]=0$ and $\small \left [ \hat{L}^{2},\frac{1}{r} \right ]=0$ .

Answer

Using eq75 and the identities $\small \left [ \hat{A},\hat{B}+\hat{C}+\hat{D} \right ]=\left [ \hat{A},\hat{B} \right ]+\left [ \hat{A},\hat{C} \right ]+\left [ \hat{A},\hat{D} \right ]$ and $\small \left [ \hat{A},\hat{B}\hat{C} \right ]=\left [ \hat{A}\hat{B} \right ]\hat{C}+\hat{B}\left[\hat{A},\hat{C} \right ]$ ,

$\small \left [ \hat{L}^{2},\hat{p}^{2} \right ]=\left [ \hat{L}_x^{\; 2}+\hat{L}_y^{\; 2}+\hat{L}_z^{\; 2},\hat{p}^{2} \right ]=0\; \; \; \; \; \; \; \; 106$

$\small \left [ \hat{L}^{2},\frac{1}{r} \right ]=\left [ \hat{L}_x^{\; 2}+\hat{L}_y^{\; 2}+\hat{L}_z^{\; 2},\frac{1}{r}\right ]=0\; \; \; \; \; \; \; \; 107$

Commutation relations of quantum orbital angular momentum operators

Question

Question

Next article: quantum orbital angular momentum ladder operators

Previous article: quantum orbital angular momentum operators (spherical coordinates)

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply