Raoult’s Law states that the partial vapour pressure of each volatile component in an ideal solution at equilibrium is equal to the product of its mole fraction in the liquid phase and the vapour pressure of the pure component at the same temperature. Mathematically:
where:
is the partial vapour pressure of component
is the mole fraction of component in the liquid
is the vapour pressure of pure component
It is named after François-Marie Raoult, a French chemist who formulated it in the 1880s. Through his experiments on the vapour pressures of solutions, Raoult discovered that the presence of a non-volatile solute lowers the vapour pressure of the solvent in proportion to its mole fraction. His work laid the groundwork for colligative properties and was pivotal in the development of solution thermodynamics.
Let’s explain Raoult’s law in an intuitive way before we derive it from thermodynamic principles. Consider a sealed container with a pure volatile liquid A (see diagram below). At a given temperature, some molecules of A evaporate from the liquid surface into the gas phase, while other molecules of A from the gas phase condense back into the liquid. Eventually, a dynamic equilibrium is established, where the rate of evaporation equals the rate of condensation. The pressure exerted by the gaseous A at this equilibrium is the vapour pressure of pure A, .
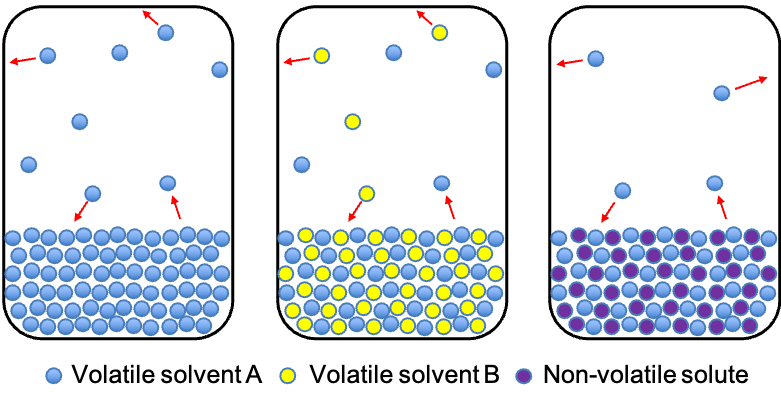
If we add another volatile liquid component B to the container, forming an ideal solution (where A and B have similar intermolecular interactions), the surface of the liquid is now shared by molecules of both A and B. This means that, for any given area of the liquid surface, fewer molecules of A can escape into the vapour phase than when A was pure. When a new equilibrium is attained, the reduced partial pressure of A is expected to be equal to the product of its mole fraction in the liquid and . The same is true for B. This is the essence of Raoult’s law. The total vapour pressure in the container is then the sum of the partial pressures of A and B:
Similarly, if we add a non-volatile solute to a container of pure A to form an ideal solution, . However, the total vapour pressure is now equal to just
, because the solute is non-volatile. Therefore, Raoult’s law can also be defined as follows: the vapour pressure of a solvent in a solution is directly proportional to its mole fraction in the liquid phase. In other words, when a non-volatile solute is added to a volatile solvent, the solvent’s vapour pressure decreases in proportion to the amount of solute present:
.
Raoult’s law can be derived from thermodynamic principles. Consider a multi-component solution with a volatile liquid A at equilibrium with its vapour. At constant temperature eq148 becomes or its molar form
. Substituting the ideal gas law in the molar form and integrating gives:
which leads to:
Substituting eq149a in eq179 yields
The equivalent expression for the chemical potential of the liquid-phase of A is
where is the mole fraction of A in the solution (see below for a complete derivation of eq181).
When a liquid and its vapour are in equilibrium, their chemical potentials are equal. Hence, , or
which rearranges to give the Raoult’s law because .

Question
Show that .
Answer
For a pure liquid A in equilibrium with its vapour, and
in eq182, which simplifies to
.
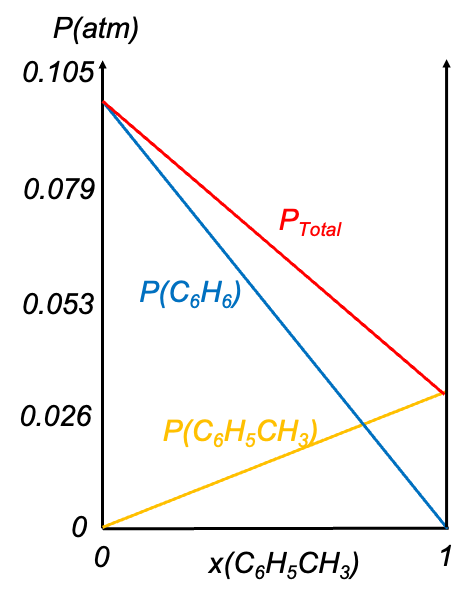
Raoult’s Law is most accurate when applied to ideal solutions, where the intermolecular forces between unlike molecules closely resemble those between like molecules. A classic example is the binary mixture of benzene and toluene, which closely follows Raoult’s Law. When the vapour pressure of toluene is plotted against its mole fraction in the solution, the resulting graph is a straight line, consistent with eq178. A similar linear plot can be made for benzene, using the inverse relationship between its mole fraction and that of toluene. The total vapor pressure of the ideal solution is obtained by summing the partial vapour pressures of both components, as illustrated in the diagram below.
However, the law fails or becomes less accurate for non-ideal solutions, in which the components interact more strongly or more weakly with each other than with themselves. An example is the acetone-chloroform system, where hydrogen bonding causes deviations from ideal behaviour (see diagram below).

Vapour pressure diagrams allow for a straightforward determination of the partial vapour pressure of each component and the total vapour pressure of the solution at a specific temperature. They also provide a basis for plotting boiling point diagrams and ultimately phase diagrams of mixtures.

Question
Derive eq181.
Answer
Consider a system with moles of solvent A and
moles of solute B forming an ideal solution.
is the Avogadro constant and the total number of moles is
. From eq147, the change in Gibbs free energy upon mixing the two components is given by:
. Since A and B have similar intermolecular interactions, there is no net release or absorption of heat upon mixing. So,
and
.
The number of ways, , to arrange
molecules of A and
molecules of B in a container with
total sites is given by the multinomial permutation:
Substituting into the statistical entropy formula of eq30 yields
, since
. Applying Stirling’s approximation (
) for large
and rearranging gives
where we have used (see this article for derivation ),
and
for the last equality.
Substituting eq183 into results in
The change in Gibbs energy upon mixing is
Substituting eq153 into the above equation yields
Equating eq184 and eq185:
For eq186 to hold, the coefficients of and
on both sides must be equal. Therefore,
and
, with the general formula being eq181.