The recurrence relations of the associated Legendre polynomials describe how each polynomial in the sequence can be obtained from its predecessors.
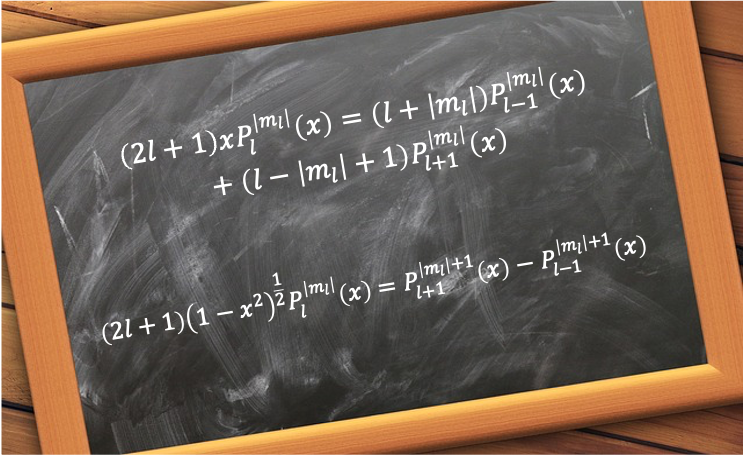
Some useful recurrence relations of the associated Legendre polynomials in quantum chemistry are:
To derive eq370, we differentiate eq366 with respect to and rearrange the result to give
Substituting eq366 in the RHS of the above equation yields
which can be rearranged to
Collecting coefficients with the same powers of ,
Comparing the equations, we have
which is eq370, where .
To derive eq371, we differentiate eq346c times with respect to
to give
. Multiplying through by
and substituting eq363a in the resultant equation gives eq371.