Rotation operator

A rotation operator $\hat{D}_k(\alpha)$ is a unitary operator that rotates quantum states by an angle $\alpha$ about an axis in a Hilbert space.

Mathematically, it is given by:

$\hat{D}_k(\alpha)=e^{-i\alpha\hat{J}_k}\;\;\;\;\;\;\;\;100$

where $\hat{J}_k$ , the angular momentum operator, is the generator of rotations about axis $k$ .

To derive eq100, we begin by noting that the probability outcome of a quantum mechanical measurement is described by the Born interpretation:

$\vert\langle\phi\vert\psi\rangle\vert^2$

where $\phi$ and $\psi$ are wavefunctions representing quantum states.

Since rotations are symmetry operations that do not change physical probabilities, we require:

$\vert\langle\hat{D}_k\phi\vert\hat{D}_k\psi\rangle\vert^2=\vert\langle\phi'\vert\psi'\rangle\vert^2=\vert\langle\phi\vert\psi\rangle\vert^2$

Using the matrix identity $(ABC\cdots)^{\dagger}=\cdots C^{\dagger}B^{\dagger}A^{\dagger}$ (see property 13 of this article for proof), we have $\vert\langle\hat{D}_k\phi\vert\hat{D}_k\psi\rangle\vert^2=\vert\langle\phi\vert\hat{D}_k^{\dagger}\hat{D}_k\vert\psi\rangle\vert^2=\vert\langle\phi\vert\psi\rangle\vert^2$ . Therefore, $\hat{D}_k$ is unitary, where $\hat{D}_k^{\dagger}\hat{D}_k=\hat{I}$ .

Let’s approximate $\hat{D}_k$ as a power series of a small change in $\alpha$ :

$\hat{D}_k(\delta\alpha)\approx\hat{D}_k(0)+\delta\alpha\hat{G}_k+(\delta\alpha)^2\hat{O}_k+\cdots\;\;\;\;\;\;\;\;101$

where $\hat{G}_k$ and $\hat{O}_k$ are first and second order rotation generator matrices respectively.

Since a rotation by zero angle must do nothing, $\hat{D}_k(0)=\hat{I}$ , and eq101 (ignoring higher order terms) becomes

$\hat{D}_k(\delta\alpha)\approx\hat{I}+\delta\alpha\hat{G}_k\;\;\;\;\;\;\;\;102$

To preserve unitarity, $(\hat{I}+\delta\alpha\hat{G}_k)^{\dagger}(\hat{I}+\delta\alpha\hat{G}_k)=\hat{I}$ . Expanding this equation and ignoring higher-order terms gives $\hat{I}+\delta\alpha\hat{G}_k^{\dagger}+\delta\alpha\hat{G}_k=\hat{I}$ or $\hat{G}_k^{\dagger}=-\hat{G}_k$ . This implies that $\hat{G}_k$ is not Hermitian, which contradicts the postulate that all physical observables in quantum mechanics are represented by Hermitian operators. It follows that eq102 must have the following form:

$\hat{D}_k(\delta\alpha)=\hat{I}-i\delta\alpha\hat{G}_k\;\;\;\;\;\;\;\;103$

For a quantum mechanical operator $\hat{A}$ to represent the same physical observable in the passively rotated frame, its expectation value must be the same whether calculated in the initial frame or with respect to the new frame:

$\langle\psi'\vert\hat{A}'\vert\psi'\rangle=\langle\psi\vert\hat{A}\vert\psi\rangle\;\;\;\;\;\;\;\;104$

Substituting $\vert\psi'\rangle=\hat{D}_k\vert\psi\rangle$ into eq104 gives $\langle\psi\vert\hat{D}_k^{\dagger}\hat{A}'\hat{D}_k\vert\psi\rangle=\langle\psi\vert\hat{A}\vert\psi\rangle$ , which means that $\hat{A}$ and $\hat{A}'$ are related by the similarity transformation $\hat{D}_k^{\dagger}\hat{A}'\hat{D}_k=\hat{A}$ or equivalently,

$\hat{A}'=\hat{D}_k\hat{A}\hat{D}_k^{\dagger}\;\;\;\;\;\;\;\;105$

where $\hat{D}_k^{\dagger}=\hat{D}_k^{-1}$ because $\hat{D}_k^{\dagger}\hat{D}_k=\hat{I}$ .

Substituting eq103 into eq105 yields:

$\hat{\boldsymbol{\mathit{r}}}'=(\hat{I}-i\delta\alpha\hat{G}_k)\hat{\boldsymbol{\mathit{r}}}(\hat{I}+i\delta\alpha\hat{G}_k)\;\;\;\;\;\;\;\;106$

where we have let the operator be the position operator $\hat{\boldsymbol{\mathit{r}}}$ .

Expanding eq106 and ignoring higher order terms results in $\hat{\boldsymbol{\mathit{r}}}'=\hat{\boldsymbol{\mathit{r}}}+i\boldsymbol{\mathit{r}}\hat{G}_k\delta\alpha-i\hat{G}_k\hat{\boldsymbol{\mathit{r}}}\delta\alpha$ , or equivalently,

$\delta\hat{\boldsymbol{\mathit{r}}}=-i\[\hat{G}_k,\hat{\boldsymbol{\mathit{r}}}\]\delta\alpha\;\;\;\;\;\;\;\;107$

where $\delta\hat{\boldsymbol{\mathit{r}}}=\hat{\boldsymbol{\mathit{r}}}'-\hat{\boldsymbol{\mathit{r}}}$ .

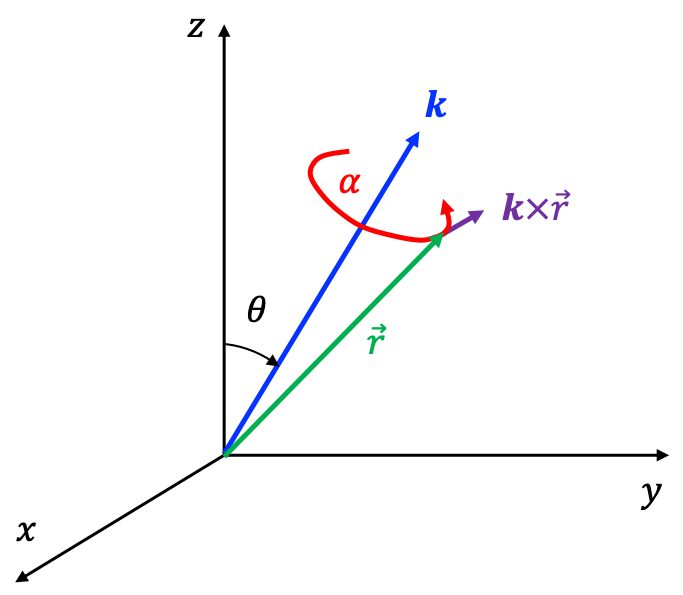
To determine the nature of $\hat{G}_k$ , we refer to the active classical rotation of the vector $\vec{r}$ by an infinitesimal angle $\delta\alpha$ about an arbitrary axis represented by the unit vector $\boldsymbol{\mathit{k}}$ (see diagram above), with the infinitesimal change in $\vec{r}$ given by:

$\delta\vec{r}=\delta\alpha(\boldsymbol{\mathit{k}}\times\vec{r})\;\;\;\;\;\;\;\;108$

where the cross product results in a vector with a magnitude proportional to $\delta\alpha$ and a direction tangential to the path of rotation.

Using the methodology of replacing classical variables with their quantum mechanical analogues to derive quantum mechanical expressions, eq108 becomes:

$\delta\hat{\boldsymbol{\mathit{r}}}=-\delta\alpha(\boldsymbol{\mathit{k}}\times\hat{\boldsymbol{\mathit{r}}})\;\;\;\;\;\;\;\;109$

where we have added a minus sign because $\delta\vec{r}$ in eq108 is defined by an active rotation about the axis, while $\delta\hat{\boldsymbol{\mathit{r}}}$ in eq107 describes a passive rotation about the axis.

Question

Why is an active rotation and a passive rotation related by a negative sign in eq109?

Answer

An active rotation refers an anticlockwise rotation of a position vector in a fixed coordinate system by the angle $\theta$ (see this article for details). In a passive rotation, the position vector remains stationary while the coordinate system rotates around it. To produce the same effect on the coordinates, a passive rotation corresponds to an anticlockwise rotation of the coordinate system by $-\theta$ . In other words, a passive rotation of the coordinate system by $-\theta$ has the same result as an active rotation of the vector by $\theta$ . Therefore, $\delta\vec{r}=\delta\alpha(\boldsymbol{\mathit{k}}\times\vec{r})=\delta\alpha\vert\boldsymbol{\mathit{k}}\vert\vert\vec{r}\vert sin\theta=-\delta\hat{\boldsymbol{\mathit{r}}}$ .

Substituting $\hat{\boldsymbol{\mathit{r}}}=\hat{x}\boldsymbol{\mathit{i}}+\hat{y}\boldsymbol{\mathit{j}}+\hat{z}\boldsymbol{\mathit{k}}$ into eq109 and expanding it gives:

$\delta\hat{x}\boldsymbol{\mathit{i}}+\delta\hat{y}\boldsymbol{\mathit{j}}+\delta\hat{z}\boldsymbol{\mathit{k}}=-\delta\alpha\hat{x}(\boldsymbol{\mathit{k}}\times\boldsymbol{\mathit{i}})-\delta\alpha\hat{y}(\boldsymbol{\mathit{k}}\times\boldsymbol{\mathit{j}})-\delta\alpha\hat{z}(\boldsymbol{\mathit{k}}\times\boldsymbol{\mathit{k}})$

Since $\boldsymbol{\mathit{k}}\times\boldsymbol{\mathit{i}}=\boldsymbol{\mathit{j}}$ , $\boldsymbol{\mathit{k}}\times\boldsymbol{\mathit{j}}=-\boldsymbol{\mathit{i}}$ and $\boldsymbol{\mathit{k}}\times\boldsymbol{\mathit{k}}=\boldsymbol{\mathit{0}}$ , we have:

$\delta\hat{x}\boldsymbol{\mathit{i}}+\delta\hat{y}\boldsymbol{\mathit{j}}+\delta\hat{z}\boldsymbol{\mathit{k}}=\delta\alpha\hat{y}\boldsymbol{\mathit{i}}-\delta\alpha\hat{x}\boldsymbol{\mathit{j}}\;\;\;\;\;\;\;\;110$

Substituting $\hat{\boldsymbol{\mathit{r}}}=\hat{x}\boldsymbol{\mathit{i}}+\hat{y}\boldsymbol{\mathit{j}}+\hat{z}\boldsymbol{\mathit{k}}$ into 107 and setting $\boldsymbol{\mathit{k}}$ to be the $z$ -axis for simplicity gives:

$\delta\hat{x}\boldsymbol{\mathit{i}}+\delta\hat{y}\boldsymbol{\mathit{j}}+\delta\hat{z}\boldsymbol{\mathit{k}}=-i\[\hat{G}_z,\hat{x}\]\delta\alpha\boldsymbol{\mathit{i}}-i\[\hat{G}_z,\hat{y}\]\delta\alpha\boldsymbol{\mathit{j}}-i\[\hat{G}_z,\hat{z}\]\delta\alpha\boldsymbol{\mathit{k}}\;\;\;\;\;\;\;\;111$

Comparing eq110 with eq111 yields:

$\[\hat{G}_z,\hat{x}\]=i\hat{y}$

$\[\hat{G}_z,\hat{y}\]=-i\hat{x}$

$\[\hat{G}_z,\hat{z}\]=0$

Comparing these three commutation relations with the total angular commutation relations of $\[\hat{J}_z,\hat{x}\]=i\hbar\hat{y}$ , $\[\hat{J}_z,\hat{y}\]=-i\hbar\hat{x}$ and $\[\hat{J}_z,\hat{z}\]=0$ , we find that $\hat{G}_k=\hat{J}_k/\hbar$ . In other words, $\hat{G}_k$ is the $k$ -th component of the total angular momentum operator, expressed in units of $\hbar$ .

A finite rotation by an angle $\alpha$ can be constructed by apply $N$ successive infinitesimal rotations, each by an angle $\delta\alpha=\alpha/N$ . From eq103,

$\hat{D}_k(\delta\alpha)=\lim_{N\rightarrow\infty}\biggr\[\hat{I}-i\frac{\alpha}{N\hbar}\hat{J}_k\biggr\]^N\;\;\;\;\;\;\;\;112$

Question

Show that $e^x=\lim_{n\rightarrow\infty}\biggr$1+\frac{x}{n}\biggr$^n$ .

Answer

Let $f(n)=\biggr$1+\frac{x}{n}\biggr$^n$ . So, $lnf(n)=nln\biggr$1+\frac{x}{n}\biggr$$ . Using the Taylor series $ln(1+y)=y-\frac{y^2}{2}+\frac{y^3}{3}+\cdots$ for small $y$ , we have

$lnf(n)=n\biggr\[\frac{x}{n}-\frac{1}{2}\biggr$\frac{x}{n}\biggr$^2+\cdots\biggr\]=x-\frac{x^2}{2n}+\cdots$

As $n\rightarrow\infty$ , we find that $lnf(n)\rightarrow x$ , or equivalently, $f(n)\rightarrow e^x$ . So, $e^x=\lim_{n\rightarrow\infty}\biggr$1+\frac{x}{n}\biggr$^n$ . This makes eq112 the definition of the matrix exponential function.

Therefore, eq112 becomes:

$\hat{D}_k(\delta\alpha)=e^{-i\frac{\alpha}{\hbar}\hat{J}_k}\;\;\;\;\;\;\;\;113$

Eq113 is usually written as:

$\hat{D}_k(\delta\alpha)=e^{-i\alpha\hat{J}_k}\;\;\;\;\;\;\;\;114$

where the eigenvalues of $\hat{J}_k$ and hence $\hat{D}_k$ are expressed in units of $\hbar$

Since $\hat{J}_k$ is a finite-dimensional linear operator acting on a finite-dimensional vector space, $e^{-i\alpha\hat{J}_k}$ can be represented by an $n\times n$ matrix in both group theory and quantum mechanical calculations. In general, the rotation operator in an Euler angle system, which is defined by three successive rotations by the angles $\phi$ , $\theta$ and $\chi$ , is given by:

$\hat{D}(\phi,\theta,\chi)=e^{-i\phi\hat{J}_z}e^{-i\theta\hat{J}_y}e^{-i\chi\hat{J}_z}\;\;\;\;\;\;\;\;115$

where $0\leq\phi\leq2\pi$ , $0\leq\theta\leq \pi$ and $0\leq\chi\leq2\pi$ .

The application of eq115 involves the rotation operator transforming a quantum state $\vert J,K\rangle$ with total angular momentum projection along the molecular axis into a linear combination of states $\vert J,M_J\rangle$ with the projection along the lab $c$ -axis:

$\hat{D}(\phi,\theta,\chi)\vert J,K\rangle=\sum_{M_J}D^J_{M_J,K}(\phi,\theta,\chi)\vert J,M_J\rangle$

where $D^J_{M_J,K}(\phi,\theta,\chi)$ , the entries of the Wigner D-matrix, are the coefficients of $\vert J,M_J\rangle$ .

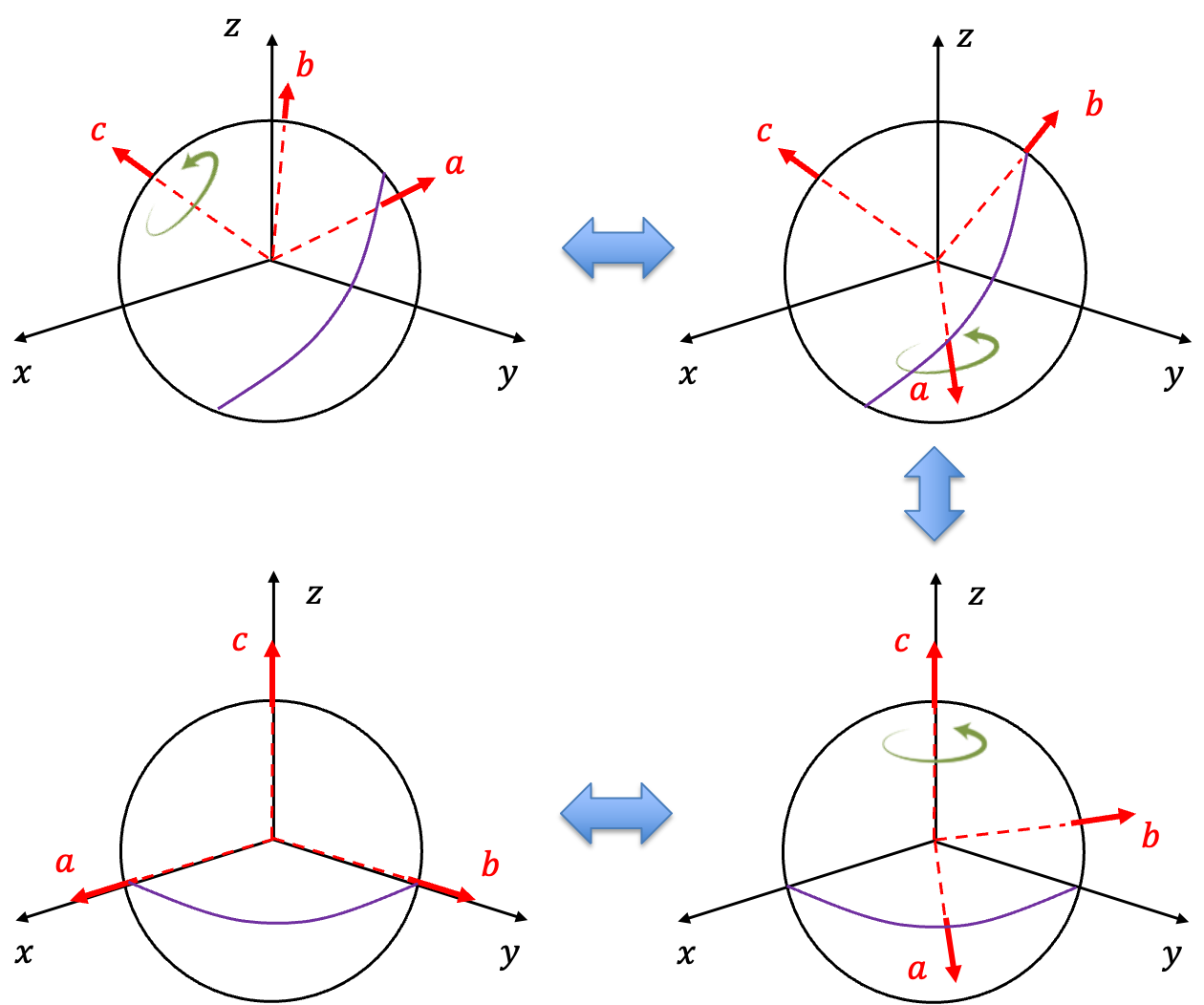
Question

Why is the transformed state a linear combination of $\vert J,M_J\rangle$ ?

If eq114 describes an operator that rotates quantum states by an angle $\alpha$ about an axis $k$ in a Hilbert space, how do three consecutive rotations described by eq115 ensure the complete transformation from the molecular coordinate system to the lab coordinate system?

Answer

In quantum mechanics, the states $\vert J,M_J\rangle$ form a complete orthonormal basis in the Hilbert space corresponding to a fixed $J$ . Therefore, any state with total angular momentum $J$ , including the rotated state $\hat{D}(\phi,\theta,\chi)\vert J,K\rangle$ , can be expressed as a linear combination of the basis states $\vert J,M_J\rangle$ .

In the diagram above, $a,b,c$ represent the molecular axes, while $x,y,z$ represent the lab-frame axes. Without assuming any specific rotation convention, the diagram illustrates that any target orientation can be achieved through three consecutive rotations. The first rotation about $c$ brings $a$ into the $xy$ -plane. The second rotation, about $a$ , aligns $c$ with $z$ . Finally, the last rotation about $c$ aligns the remaining axes of the two coordinate systems.

Question

Answer

Question

Answer

Question

Answer

Next article: Wigner D-matrix

Previous article: Centrifugal distortion

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply