Selection rules for vibration-rotation transitions

The selection rules for vibration-rotation transitions govern which simultaneous changes in vibrational and rotational energy levels are allowed when a molecule absorbs or emits infrared radiation.

These rules arise from quantum mechanical principles and the requirement that transitions involve a change in the molecule’s electric dipole moment $\boldsymbol{\mathit{\mu}}$ , and they combine the selection rules for pure vibrational and pure rotational transitions.

In determining the selections rules for pure vibrational and pure rotational transitions, we evaluated conditions under which $\langle\psi_v'\vert\boldsymbol{\mathit{\mu}}\vert\psi_v\rangle\neq 0$ and $\langle\psi_r'\vert\boldsymbol{\mathit{\mu}}\vert\psi_r\rangle\neq 0$ separately. However, the selection rules for vibration-rotation transitions require that $\langle\psi_v'\psi_r'\vert\boldsymbol{\mathit{\mu}}\vert\psi_v\psi_r\rangle\neq 0$ . To show that this ultimately reduces to the selection rules for pure vibrational and pure rotational transitions, we begin with

$\boldsymbol{\mathit{\mu}}=\mu_x\boldsymbol{\mathit{e}}_x+\mu_y\boldsymbol{\mathit{e}}_y+\mu_z\boldsymbol{\mathit{e}}_z=\mu_a\boldsymbol{\mathit{e}}_a+\mu_b\boldsymbol{\mathit{e}}_b+\mu_c\boldsymbol{\mathit{e}}_c\;\;\;\;\;\;\;\;1$

where $x$ , $y$ and $z$ are the orthogonal lab-frame axes; $a$ , $b$ and $c$ are the orthogonal principal axes of inertia of the molecule (molecular frame); and the $\boldsymbol{\mathit{e}}$ ’s are unit vectors along the axes.

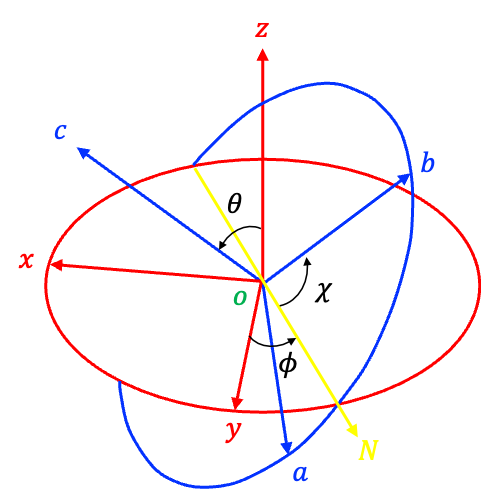
The relationship between the two frames is shown in the diagram above, with the origin $o$ of both frames commonly placed at the centre of mass of the molecule. The lab-frame is stationary in space and does not rotate with the molecule, whereas the molecular frame moves with the molecule and rotates as it does. $N$ , known as the line of nodes, denotes the line passing through the intersections of the $xy$ and $ab$ planes. The orientation of the molecular frame with respect to the lab frame is described by the Euler angles $0\leq\theta\leq\pi$ , $0\leq\phi\leq 2\pi$ , and $0\leq\chi\leq 2\pi$ .

From eq1,

$\mu_z=\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{\mu}}=\mu_a cos(\angle zoa)+\mu_b cos(\angle zob)+\mu_c cos(\angle zoc)\;\;\;\;\;\;\;\;2$

where $cos(\angle zoa)=\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{e}}_a$ , $cos(\angle zob)=\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{e}}_b$ and $cos(\angle zoc)=\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{e}}_c$ .

Similarly, $\mu_y=\mu_a cos(\angle yoa)+\mu_b cos(\angle yob)+\mu_c cos(\angle yoc)$ and $\mu_x=\mu_a cos(\angle xoa)+\mu_b cos(\angle xob)+\mu_c cos(\angle xoc)$ . However, we can simplify the analysis to $\mu_z$ , which can always be arbitrarily chosen as the polarisation direction of the incident oscillating radiation.

To express the cosines in terms of the Euler angles, we need to derive the full rotation matrix according to the convention of a specific sequence of three consecutive elemental rotations to describe any 3D orientation.

The first rotation is about the lab-frame $z$ -axis by $\phi$ :

$R_z\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}cos\phi&-sin\phi&0\\sin\phi&cos\phi&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}x'\\y'\\z'\end{pmatrix}$

The second rotation is about the $y'$ axis, also known as the line of nodes $N$ , by $\theta$ . It lies in the initial $xy$ -plane but is fixed in its direction after the first rotation and is perpendicular to both the initial $z$ -axis and the final $c$ -axis:

$R_N\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}cos\theta&0&-sin\theta\\0&1&0\\sin\theta&0&cos\theta\end{pmatrix}\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}x''\\y''\\z''\end{pmatrix}$

The last rotation is about the $z''$ axis, which is also the molecular $c$ -axis, by $\chi$ :

$R_c\begin{pmatrix}x''\\y''\\z''\end{pmatrix}=\begin{pmatrix}cos\chi&-sin\chi&0\\sin\chi&cos\chi&0\\0&0&1\end{pmatrix}\begin{pmatrix}x''\\y''\\z''\end{pmatrix}=\begin{pmatrix}a\\b\\c\end{pmatrix}$

Therefore, the full rotation matrix is:

$R=R_zR_NR_c=\begin{pmatrix}cos\phi cos\theta cos\chi-sin\phi sin\chi&-cos\phi cos\theta sin\chi-sin\phi cos\chi&-cos\phi sin\theta\\sin\phi cos\theta cos\chi+cos\phi sin\chi&-sin\phi cos\theta sin\chi+cos\phi cos\chi&-sin\phi sin\theta\\sin\theta cos\chi&-sin\theta sin\chi&cos\theta\end{pmatrix}$

A rotation matrix is the transpose of the change of basis matrix $R^T$ , which in this case is

$R^T=\begin{pmatrix}\boldsymbol{\mathit{e}}_a\cdot\boldsymbol{\mathit{e}}_x&\boldsymbol{\mathit{e}}_a\cdot\boldsymbol{\mathit{e}}_y&\boldsymbol{\mathit{e}}_a\cdot\boldsymbol{\mathit{e}}_z\\\boldsymbol{\mathit{e}}_b\cdot\boldsymbol{\mathit{e}}_x&\boldsymbol{\mathit{e}}_b\cdot\boldsymbol{\mathit{e}}_y&\boldsymbol{\mathit{e}}_b\cdot\boldsymbol{\mathit{e}}_z\\\boldsymbol{\mathit{e}}_c\cdot\boldsymbol{\mathit{e}}_x&\boldsymbol{\mathit{e}}_c\cdot\boldsymbol{\mathit{e}}_y&\boldsymbol{\mathit{e}}_c\cdot\boldsymbol{\mathit{e}}_z\end{pmatrix}$

Therefore,

$R^T=\begin{pmatrix}\boldsymbol{\mathit{e}}_x\cdot\boldsymbol{\mathit{e}}_a&\boldsymbol{\mathit{e}}_x\cdot\boldsymbol{\mathit{e}}_b&\boldsymbol{\mathit{e}}_x\cdot\boldsymbol{\mathit{e}}_c\\\boldsymbol{\mathit{e}}_y\cdot\boldsymbol{\mathit{e}}_a&\boldsymbol{\mathit{e}}_y\cdot\boldsymbol{\mathit{e}}_b&\boldsymbol{\mathit{e}}_y\cdot\boldsymbol{\mathit{e}}_c\\\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{e}}_a&\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{e}}_b&\boldsymbol{\mathit{e}}_z\cdot\boldsymbol{\mathit{e}}_c\end{pmatrix}$

and eq2 becomes

$\mu_z=\mu_asin\theta cos\chi-\mu_bsin\theta sin\chi+\mu_ccos\theta\;\;\;\;\;\;\;\;3$

We can also determine $\mu_x$ and $\mu_y$ in terms of the Euler angles by repeating the steps above.

Now, certain vibrational motions change a molecule’s electric dipole moment, such that $\frac{d\boldsymbol{\mathit{\mu}}}{dQ}\neq 0$ , where $Q$ represents the normal coordinates typically used to describe vibrational motions. Similarly, rotational motions also affect the dipole moment, with $\frac{d\boldsymbol{\mathit{\mu}}}{d\Omega}\neq 0$ , where $\Omega$ collectively denotes the Euler angles. This implies that the dipole moment is a function of both $Q$ and $\Omega$ , i.e. $\boldsymbol{\mathit{\mu}}(Q,\Omega)$ . Since the components $\mu_a$ , $\mu_b$ and $\mu_c$ in eq3 are projections of $\boldsymbol{\mathit{\mu}}$ onto the molecular axes, which rotate with the molecule, they are independent of the Euler angles, and must therefore be functions of $Q$ alone.

If we assume that the atoms in the molecule vibrate with a small amplitude about their equilibrium positions, we can expand $\mu_a$ , $\mu_b$ and $\mu_c$ in a Taylor series, e.g.

$\mu_a=\mu_{a,e}+\sum_{k=1}^f\biggr$\frac{\partial \mu_a}{\partial Q_k}\biggr$_eQ_k+\cdots\;\;\;\;\;\;\;\;4$

where $f=3N-6$ for non-linear polyatomic molecules and $f=3N-5$ for linear molecules.

Substituting eq4 (by ignoring the higher terms) and the corresponding expansions for $\mu_b$ and $\mu_c$ into $\langle\psi_v'\psi_r'\vert\mu_z\vert\psi_v\psi_r\rangle$ gives:

$\begin{align}\langle\psi_v'\psi_r'\vert\mu_z\vert\psi_v\psi_r\rangle &=\biggr$\int\psi_v^{*'}\psi_vdQ\biggr$\[\mu_{a,e}I_a-\mu_{b,e}I_b+\mu_{c,e}I_c\]\\&+\sum_{k=1}^f\biggr$\int\psi_v^{*'}Q_k\psi_vdQ\biggr$\biggr\[\biggr$\frac{\partial\mu_a}{\partial Q_k}\biggr$_eI_a-\biggr$\frac{\partial\mu_b}{\partial Q_k}\biggr$_eI_b+\biggr$\frac{\partial\mu_c}{\partial Q_k}\biggr$_eI_c\biggr\]\;\;\;\;\;\;\;\;5\end{align}$

where

$\int\psi_v^{*'}\psi_vdQ=\prod_{k=1}^f\int\psi_k^{*'}\psi_kdQ_k$ .
$I_a=\int\psi_r^{*'}\psi_rsin\theta cos\chi d\tau_r$ .
$I_b=\int\psi_r^{*'}\psi_rsin\theta sin\chi d\tau_r$ .
$I_c=\int\psi_r^{*'}\psi_rcos\theta d\tau_r$ .
$d\tau_r=sin\theta d\theta d\phi d\chi$ .

Question

Why is $d\tau_r=sin\theta d\theta d\phi d\chi$ ?

Answer

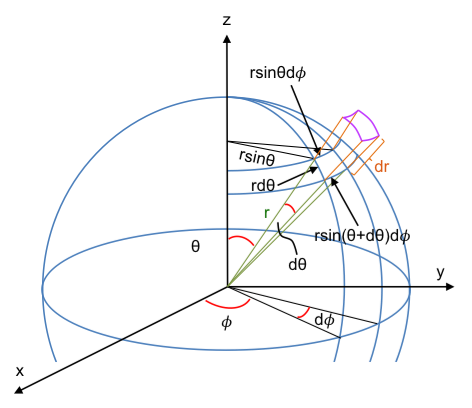
Consider an arrow in a 3D space. To fully describe its rotation, we must determine its complete orientation. This is achieved by pointing the arrow in a certain direction and spinning it around its shaft. In other words, we must first specify the direction of a chosen axis of a 3D object (like the arrow’s shaft), and then the rotation about that axis to describe its rotation. In the Euler angle framework, the first two angles $\theta$ and $\phi$ define a direction on the unit sphere (like latitude and longitude on Earth). Small changes to this direction are expressed as $sin\theta d\theta d\phi$ (see diagram below, where $r=1$ ). The third angle $\chi$ determines the extent of rotation around that direction. Therefore, the combined infinitesimal change in the object’s orientation in rotation space is $sin\theta d\theta d\phi d\chi$ .

Since the vibrational wavefunctions are orthonormal, the first integral on RHS of eq5 is non-zero only if $\psi_k'=\psi_k$ for all $k$ , i.e. when there is no vibrational transition. Assuming $I_a\leq I_b\leq I_c$ , the selection rules associated with this term pertain to pure rotational transitions. The second term is non-zero only if both $\int\psi_v^{*'}Q_k\psi_vdQ$ and the terms in the square bracket are non-zero. This implies that the selection rules associated with the 2^nd term correspond to those of both pure vibrational and pure rotational transitions.

For a polar linear molecule with $c$ as the molecular axis, $\mu_{a,e}=\mu_{b,e}=0$ while $\mu_{c,e}\neq 0$ , and the first term on RHS of eq5 reduces to $\mu_{c,e}I_c$ if $\psi_k'=\psi_k$ for all $k$ . Furthermore, $\biggr$\frac{\partial\mu_a}{\partial Q_k}\biggr$_e=\biggr$\frac{\partial\mu_b}{\partial Q_k}\biggr$_e=0$ for non-degenerate normal modes like stretching, but may not be zero for degenerate modes like bending. Despite that, $I_a\leq I_b\leq I_c$ and therefore, the general selection rules for vibration-rotation transitions of polar linear molecules, which require $\langle\psi_v'\psi_r'\vert\mu_z\vert\psi_v\psi_r\rangle\neq 0$ for linearly polarised light, are:

$\Delta J=\pm 1,\Delta M_J=0,\pm 1,\Delta v=\pm 1\;\;\;\;\;\;\;\;6$

In practice, eq6 is written more simply as:

$\Delta J=0,\pm 1,\Delta v=\pm 1\;\;\;\;\;\;\;\;7$

The condition $\Delta M_J=0,\pm 1$ is omitted because the $M_J$ -related fine structure is often unresolved in most experimental spectra. Additionally, the inclusion of $\Delta J=0$ highlights that total angular momentum conservation must be satisfied during a photon-mediated vibrational transition, even though $\Delta J=0$ is forbidden for most linear molecules in electric dipole transitions.

Eq7 also corresponds to be the vibration-rotation selection rules for spherical tops.

For a symmetric rotor, any allowed vibrational transition can involve a change in $\mu_{c,e}$ along the symmetry axis $c$ (known as parallel transitions), as well as changes in $\mu_{a,e}$ and $\mu_{b,e}$ , which are perpendicular to $c$ (perpendicular transitions). Since the pure rotational selection rules for a symmetric rotor (neglecting $M_J$ -related fine structure), where the permanent dipole lies along the symmetry axis, are $\Delta J=\pm 1,\Delta K=0$ , the selection rules for parallel transitions are:

$\Delta J=0,\pm 1,\Delta K=0,\Delta v=\pm 1\;\;\;\;\;\;\;\;8$

In the case of a perpendicular transition, $\mu_{a,e}\neq 0$ and $\mu_{b,e}\neq 0$ , while $\mu_{c,e}=0$ . This results in the following selection rules:

$\Delta J=0,\pm 1,\Delta K=\pm 1,\Delta v=\pm 1\;\;\;\;\;\;\;\;8a$

Question

Explain why $\Delta K=\pm 1$ for a perpendicular transition.

Answer

The rotational wavefunction can be approximated as $\psi_r=D^J_{M_JK}(\theta,\psi,\chi)=d^J_{M_JK}(\theta)e^{-M_J\phi}e^{-iK\chi}$ . Since $\mu_{a,e}\neq 0$ ,

$\mu_{a,e}I_a=\mu_{a,e}\int\psi_r^{*'}\psi_rsin\theta cos\chi d\tau_r\propto\frac{1}{2}\int^{2\pi}_0e^{iK'\chi}e^{-iK\chi}(e^{i\chi}+e^{-i\chi})d\chi$

The integral $\int_0^{2\pi}\[e^{i(K'-K+1)\chi}+e^{i(K'-K-1)\chi}\]d\chi$ is nonzero only if either exponent is zero, which happens when $K'-K+1=0$ or $K'-K-1=0$ , i.e. $\Delta K=\pm 1$ . The same logic when applied to $\mu_{b,e}\neq 0$ also results in $\Delta K=\pm 1$ .

Combining eq8 and eq8a, the general vibration-rotation selection rules for a symmetric rotor are:

$\Delta J=0,\pm 1,\Delta K=0,\pm 1,\Delta v=\pm 1\;\;\;\;\;\;\;\;8b$

Selection rules for vibration-rotation transitions

Question

Answer

Question

Answer

Next article: Vibration-rotation spectra of diatomic molecules

Content page of rovibrational spectroscopy

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply