The singlet and triplet states

The singlet state describes a composite system with a coupled spin eigenstate of $\small \vert j=0,m_j=0\rangle$ , while a triplet state refers to a composite system with coupled spin eigenstates of $\small \vert 1,+1\rangle$ , $\small \vert 1,0\rangle$ and $\small \vert 1,-1\rangle$ .

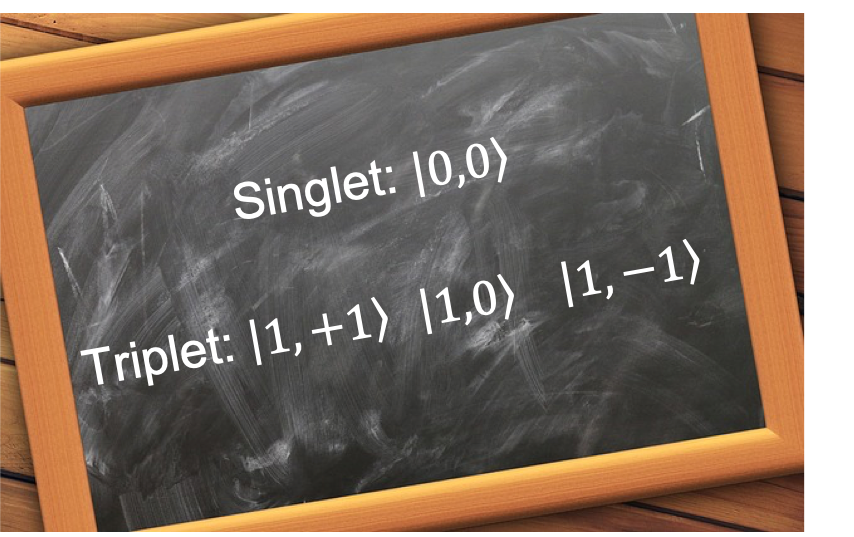
Consider a system of two spin- $\small \frac{1}{2}$ particles ( $\small s_1=\frac{1}{2}$ and $\small s_2=\frac{1}{2}$ ). According to the Clebsch-Gordan series, the allowed angular momenta of the system are $\small j=1,0$ , which implies that the system is characterised by the spin eigenstates $\small \vert 1,+1\rangle$ , $\small \vert 1,0\rangle$ , $\small \vert 1,-1\rangle$ and $\small \vert 0,0\rangle$ . The basis states forming these four spin eigenstates are given by eq193, with the general spin eigenstate of the system being a linear combination of these basis states (see eq195).

Let’s begin with the determination of the values of the coefficients for the spin eigenstates $\small \vert 1,0\rangle$ and $\small \vert 0,0\rangle$ , which must adhere to the condition: $\small \hat{S}_z^{\; (T)}\vert\psi\rangle=0\hbar\vert\psi\rangle$ . Letting the operator $\small \hat{S}_z^{\; (T)}$ act on eq195 and using eq193 and 197,

$\hat{S}_z^{\; (T)}\vert\psi\rangle=c_1\hbar\begin{pmatrix} 1\\0 \\ 0 \\ 0 \end{pmatrix}-c_4\hbar\begin{pmatrix} 0\\0 \\ 0 \\ 1 \end{pmatrix}+0\hbar\left [c_2\begin{pmatrix} 0\\1 \\ 0 \\ 0 \end{pmatrix}+c_3\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\right ]$

For the eigenvalue equation $\hat{S}_z^{\; (T)}\vert\psi\rangle=0\hbar\vert\psi\rangle$ to be valid, $c_1=c_4=0$ , i.e. one possible spin eigenstate when $m_j=0$ is $\vert\psi\rangle=c_2\vert+z\rangle_1\otimes\vert-z\rangle_2+c_3\vert-z\rangle_1\otimes\vert+z\rangle_2$ , while the other possible spin eigenstate is $\vert\psi\rangle=c_2\vert+z\rangle_1\otimes\vert-z\rangle_2-c_3\vert-z\rangle_1\otimes\vert+z\rangle_2$ . These two spin eigenstates must correspond to either $\vert 1,0\rangle$ or $\vert0,0\rangle$ . To distinguish them, we use eq203 and let the operator act on the two spin eigenstates to give:

$\hat{{S}^{2}}^{(T)}\left [ c_2\begin{pmatrix} 0\\1 \\0 \\0 \end{pmatrix}\pm c_3\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\right ] =\hbar^{2}\left [ c_2\begin{pmatrix} 0\\1 \\1 \\0 \end{pmatrix}\pm c_3\begin{pmatrix} 0\\1 \\ 1 \\ 0 \end{pmatrix}\right ]$

Since the two eigenstates are characterised by $j=1$ and $j=0$ , the expected results are $\hat{{S}^{2}}^{(T)}\vert\psi\rangle=j(j+1)\hbar^{2}\vert\psi\rangle=2\hbar^{2}\vert\psi\rangle$ and $\hat{{S}^{2}}^{(T)}\vert\psi\rangle=j(j+1)\hbar^{2}\vert\psi\rangle=0\hbar^{2}\vert\psi\rangle$ respectively. Therefore, the above equation is valid only if $c_2=c_3=c$ , such that:

$\small \hat{{S}^{2}}^{(T)}\left [ c\begin{pmatrix} 0\\1 \\0 \\0 \end{pmatrix}+ c\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\right ] =\hbar^{2}\left [ c\begin{pmatrix} 0\\1 \\1 \\0 \end{pmatrix}+ c\begin{pmatrix} 0\\1 \\ 1 \\ 0 \end{pmatrix}\right ]=2\hbar^{2}c\begin{pmatrix} 0\\1 \\ 1 \\ 0 \end{pmatrix}=2\hbar^{2}\left [ c\begin{pmatrix} 0\\1 \\0 \\0 \end{pmatrix}+ c\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\right ]$

and

$\small \hat{{S}^{2}}^{(T)}\left [ c\begin{pmatrix} 0\\1 \\0 \\0 \end{pmatrix}- c\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\right ] =\hbar^{2}\left [ c\begin{pmatrix} 0\\1 \\1 \\0 \end{pmatrix}- c\begin{pmatrix} 0\\1 \\ 1 \\ 0 \end{pmatrix}\right ]=\hbar^{2}c\begin{pmatrix} 0\\0 \\ 0 \\ 0 \end{pmatrix}=0\hbar^{2}\left [ c\begin{pmatrix} 0\\1 \\0 \\0 \end{pmatrix}- c\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix}\right ]$

Therefore, $\small \vert1,0\rangle=c(\vert+z\rangle_1\otimes\vert-z\rangle_2+\vert-z\rangle_1\otimes\vert+z\rangle_2)$ and $\small \vert0,0\rangle=c(\vert+z\rangle_1\otimes\vert-z\rangle_2-\vert-z\rangle_1\otimes\vert+z\rangle_2)$ . The spin state $\small \vert0,0\rangle$ as mentioned earlier is the singlet state, which after normalisation becomes

$\small \vert0,0\rangle=\frac{1}{\sqrt{2}}(\vert+z\rangle_1\otimes\vert-z\rangle_2-\vert-z\rangle_1\otimes\vert+z\rangle_2)\; \; \; \; \; \; \; \; 220$

Question

Show that the normalisation constant is $\small \frac{1}{\sqrt{2}}$ .

Answer

$\langle\psi\vert\psi\rangle=1\; \; \; \; \Rightarrow \; \; \; \; c^{*}\left [ \begin{pmatrix} 0\\1 \\ 0 \\ 0 \end{pmatrix}-\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix} \right ] ^{\dagger}c\left [ \begin{pmatrix} 0\\1 \\ 0 \\ 0 \end{pmatrix}-\begin{pmatrix} 0\\0 \\ 1 \\ 0 \end{pmatrix} \right ]=1$

$\vert c\vert^{2}\begin{pmatrix} 0 &1 &-1 &0 \end{pmatrix}\begin{pmatrix} 0\\1 \\ -1 \\ 0 \end{pmatrix}=1\; \; \; \; \Rightarrow \; \; \; \; c=\frac{1}{\sqrt{2}}$

Likewise, the state $\vert1,0\rangle$ after normalisation is

$\vert1,0\rangle=\frac{1}{\sqrt{2}}(\vert+z\rangle_1\otimes\vert-z\rangle_2+\vert-z\rangle_1\otimes\vert+z\rangle_2)\; \; \; \; \; \; \; \; 221$

We have two more spin eigenstates of the system to consider: $\vert1,+1\rangle$ and $\vert1,-1\rangle$ . Since the allowed values of the total magnetic quantum number $m_j$ are the sum of the allowed values of the two contributing magnetic quantum numbers (see eq207), $\vert1,+1\rangle=\vert+z\rangle_1\otimes\vert+z\rangle_2$ and $\vert1,-1\rangle=\vert-z\rangle_1\otimes\vert-z\rangle_2$ ., both of which are already normalised because they are basis states.

Question

Verify that $\hat{{S}^{^{2}}}^{{T}}\vert1,\pm1\rangle=2\hbar^{2}\vert1,\pm1\rangle$ and $\hat{S}_z^{\; {T}}\vert1,\pm1\rangle=\pm\hbar\vert1,\pm1\rangle$ .

Answer

Using eq203

$\hat{{S}^{2}}^{(T)}\vert1,+1\rangle=\hbar^{2}\begin{pmatrix} 2 &0 &0 &0 \\ 0 &1 &1 &0 \\ 0& 1 & 1 & 0\\ 0& 0& 0& 2 \end{pmatrix}\begin{pmatrix} 1\\0 \\ 0 \\ 0 \end{pmatrix}=2\hbar^{2}\begin{pmatrix} 1\\0 \\ 0 \\ 0 \end{pmatrix}$

Similarly, $\hat{{S}^{2}}^{(T)}\vert1,-1\rangle=2\hbar^{2}\vert1,-1\rangle$ . Using eq197,

$\hat{S}_z^{\; {T}}\vert1,+1\rangle=\hbar\begin{pmatrix} 1 &0 &0 &0 \\ 0 &0 &0 &0 \\ 0& 0 & 0 & 0\\ 0& 0& 0& -1 \end{pmatrix}\begin{pmatrix} 1\\0 \\ 0 \\ 0 \end{pmatrix}=\hbar\begin{pmatrix} 1\\0 \\ 0 \\ 0 \end{pmatrix}$

Similarly, $\hat{S}_z^{\; (T)}\vert1,-1\rangle=-\hbar\vert1,-1\rangle$ .

Therefore, we have:

$Triplet\: state=\left\{\begin{matrix} \vert1,+1\rangle&=\vert+z\rangle_1\otimes\vert+z\rangle_2 \\ \vert1,0\rangle &=\frac{1}{\sqrt{2}}(\vert+z\rangle_1\otimes\vert-z\rangle_2+\vert-z\rangle_1\otimes\vert+z\rangle_2)\\ \vert1,-1\rangle&=\vert-z\rangle_1\otimes\vert-z\rangle_2 \end{matrix}\right.$

$Singlet\: state=\vert0,0\rangle=\frac{1}{\sqrt{2}}[\vert+z\rangle_1\otimes\vert-z\rangle_2-\vert-z\rangle_1\otimes\vert+z\rangle_2]$

or in the wave function notation:

$Triplet\: state=\left\{\begin{matrix} \sigma_a&=\alpha(1)\alpha(2)\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; 222 \\ \sigma_b &=\frac{1}{\sqrt{2}}[\alpha(1)\beta(2)+\beta(1)\alpha(2)]\; \; \; \; \; \; 223\\ \sigma_c&=\beta(1)\beta(2)\; \; \; \; \; \; \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; 224 \end{matrix}\right.$

$Singlet\: state=\sigma_d=\frac{1}{\sqrt{2}}[\alpha(1)\beta(2)-\beta(1)\alpha(2)]\; \; \; \; \; \; \; \; 225$

The helium atom with the excited state configuration of 1s¹2s¹ is commonly used to illustrate the singlet and triplet states. If the electrons have anti-parallel spins, the excited atom is characterised by the singlet state. If the electrons have parallel spins, the excited helium is in the triplet state.

The singlet and triplet states

Question

Answer

Question

Answer

Next article: quantum entanglement

Previous article: composite systems – beyond spin operators

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply