The SO(3) group, or special orthogonal group in three dimensions, is an infinite group of all 3D rotations.
Each element of the group corresponds to a rotation operator, characterised by a unit rotation axis and an angle
. Since there are infinitely many possible rotation angles and axes, SO(3) contains infinitely many elements. These elements satisfy the properties of a group. For example, the binary operation of two rotation operators, each with a specific rotation angle about an axis, results in another rotation operator, demonstrating the closure property.
Consider the rotation of the spherical harmonics around the -axis. When the rotation operator
acts on
by an angle
around the
-axis, only the azimuthal angle
is affected and each basis is transformed into
. The transformation for all basis functions is summarised as:

Question
Prove that if , then
.
Answer
Consider the Taylor series of the exponential function . Since
We have
In other words, , and according to the above Q&A,
where is the
-component of the angular momentum operator, expressed in
units.
Since an irreducible representation of a group is expressed by a set of matrices (or matrix-valued functions) that represent the group elements as linear operators on a vector space, an irreducible representation of the SO(3) group is –dimensional (see eq120), with the set
forming a basis for the irreducible representation for a fixed
.

Question
Why does the matrix representation of about the
-axis belong to an irreducible representation of SO(3) when it is diagonal?
Answer
An irreducible representation is a group representation whose matrices cannot be simultaneously transformed, via the same invertible similarity transformation, into block diagonal form. For SO(3), an irreducible representation consists of matrices representing rotation operators about different axes. Even though the matrix of about the
-axis is diagonal, which implies reducibility on its own, other matrices in the same representation, such as
about the
-axis, contain non-zero off-diagonal elements. These non-diagonal matrices cannot all be simultaneously diagonalised by the same similarity transformation. Therefore, the matrix representation of
about the
-axis belongs to an irreducible representation of SO(3).
The character of the rotation matrix is , which is a geometric series
, where
,
and
. This implies that
Using Euler’s formula of ,
The SO(3) group does not have a standard character table in the same way that finite point groups do. Its irreducible representations are labelled by a non-negative integer , which form a discrete set. However, the group elements and their associated characters are continuous functions that depend on the rotation angle.
Nevertheless, for illustrative purposes, we can express the relationships between group elements, their irreducible representations and corresponding characters in the following way:
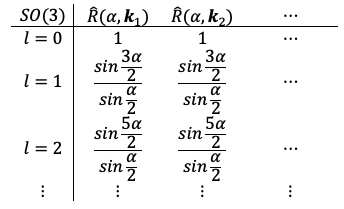
where each can be further expanded as follows:
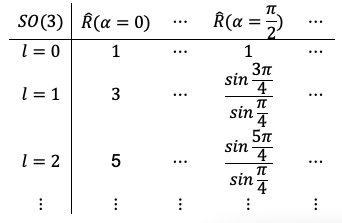

Question
Why is for
?
Answer
From eq122, for
. At
, this expression is indeterminate, but we can evaluate the limit. Substituting
into the trigonometric identity
gives
. So,
Substituting the half-angle formula into the above equation yields
. Therefore,
. Since
is represented by the identity matrix, the trace
equals the dimension of the representation of
. Using the same logic,
for
.
In general, a rotation operator of the SO(3) group is given by (see this article for derivation):
where ,
and
are the Euler angles.
The question, then, is whether the table relating the general rotation group elements, their irreducible representations and corresponding characters will be the same as that of a single-axis, single-angle rotation operator such as ?
The character of an irreducible representation of SO(3) depends only on the total rotation angle, not on the specific rotation axis or the individual Euler angles. Since SO(3) is the infinite group of all possible 3D rotations, there exists a one-to-one correspondence in symmetry between three consecutive rotations described by and a single rotation described by
. In other words, even though
is expressed in terms of Euler angles, it represents the same group element as some
, because we can always find a
symmetry operation about an appropriate axis
that produces the same
group element and therefore the same character value. Hence,
Finally, the rotation of , the Wigner D-matrix elements, for fixed
and fixed
is given by:
This shows that, for fixed , the set
forms a basis of the same
-dimensional irreducible representation of SO(3) as the set
. Since
are eigenfunctions of the angular momentum operators (
and
), it follows that
are also eigenfunctions of the corresponding operators
and
. In other words,
are also rotational wavefunctions.

Question
Elaborate on why are also eigenfunctions of
and
if
are eigenfunctions of
and
.
Answer
As mentioned earlier, (or equivalently
) is a generator of an irreducible representation of SO(3). Its matrix representation is
However, the matrix itself, is not an element of an irreducible representation of SO(3). , or any component
of the angular momentum operator, is related to the rotation operator
, by
(see eq121 for an example). Using the Taylor series definition of the exponential function yields:
Applying the commutation relation identities and
gives:
Since , where
is a constant, and
commutes with
, i.e.
, we have:
According to Schur’s first lemma, any non-zero matrix that commutes with all matrices of an irreducible representation of a group is a multiple of the identity matrix. Therefore, (or
) must be a multiple of the identity operator within the
-dimensional subspace:
When (or
) acts on any basis function
within this irreducible subspace, we obtain:
This shows that the basis functions are eigenfunctions of
and
. Similarly,
, are eigenfunctions of
and
.