The Ewald sphere is a mathematical construct that relates the geometry of the incident and scattered wave vectors to the reciprocal lattice.
Consider a crystal at A being irradiated by an incident wave vector s0, scattering a wave vector s that makes an angle 2θ with s0, thereby satisfying Bragg’s law (see diagram below).
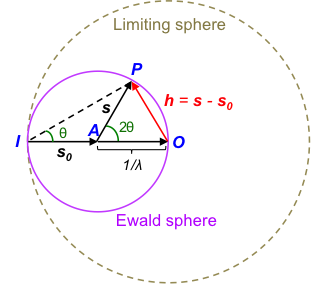
Since X-ray scattering is elastic, IsI = Is0I and the two wave vectors become radii of a sphere called the Ewald sphere. The vector OP is the reciprocal lattice vector (s – s0) that is denoted by h with the origin at O.
Since h = (s – s0), eq24 becomes
From eq11, . Substitute
and eq24f in eq24e, we have:
This means that IA = AO = AP = 1/λ. Therefore, to satisfy Bragg’s law that results in constructive interference of scattered X-rays, the head of the reciprocal lattice vector must lie on any point on the surface of the Ewald sphere. From eq24f and eq11,
Since -1 ≤ sinθ ≤ 1,
As the maximum magnitude of the reciprocal lattice vector is 2/λ, all reciprocal lattice vectors that potentially satisfy the Laue equations or Bragg’s law are enclosed in a sphere of radius known as the limiting sphere. The Ewald sphere is used to visualise different X-ray diffraction techniques including single crystal X-ray diffraction.

Question
Is the Ewald sphere really necessary? Can all diffraction patterns be discerned without the construct?
Answer
While it’s true that the fundamental condition for diffraction is Bragg’s Law or the Laue conditions, the Ewald sphere is an incredibly valuable and practically necessary construct for several key reasons:
Visualisation of Multiple Reflections: Bragg’s Law and the Laue conditions describe the diffraction from a single set of crystal planes. However, a crystal contains a vast number of different sets of planes, each with its own -spacing and orientation. The Ewald sphere provides a single, elegant way to simultaneously visualise which of these many reciprocal lattice points (representing all possible sets of planes) are in the correct orientation to satisfy the diffraction condition for a given incident X-ray wavelength and crystal orientation. Without it, you would have to consider each set of planes individually, making it much harder to grasp the overall diffraction pattern.
Understanding the Influence of Wavelength and Orientation: The Ewald sphere clearly illustrates how changing the incident X-ray wavelength (which changes the radius of the sphere) or rotating the crystal (which rotates the reciprocal lattice) affects which reflections will be observed. This is crucial for designing and interpreting diffraction experiments. When you rotate the crystal, the reciprocal lattice (which is mathematically linked to the crystal lattice) also rotates by the same amount around the origin of the reciprocal space. As the reciprocal lattice rotates, different reciprocal lattice points will, at certain crystal orientations (and thus reciprocal lattice orientations), pass through the surface of the Ewald sphere. Each time a reciprocal lattice point touches the sphere, the conditions for diffraction from the corresponding set of crystal planes are met, and a diffraction spot at a specific angle is observed. In practice, software used in X-ray diffraction experiments utilises the Ewald sphere concept to simulate diffraction patterns.
Interpretation and Indexing: The diffraction pattern observed on a detector is a projection of the reciprocal lattice points that intersect the Ewald sphere. Understanding the Ewald sphere helps in indexing these diffraction spots and relating them back to the crystal’s reciprocal lattice and ultimately its real-space structure. The software uses the Ewald sphere concept and the known or refined unit cell parameters to index the reflections, assigning the correct Miller indices (hkl) to each spot by finding the reciprocal lattice point that was in diffracting condition.
