The Miller index is a system developed by British mineralogist William Miller in 1839 for describing the orientation of lattice planes. Since a normal vector to a plane describes the orientation or direction of the plane, the Miller index of a plane must have parameters consistent with the normal vector. Recall that the scalar equation of a plane is given by eq2 of the previous section:
In the case of a space lattice, let’s rewrite it as:
where a/h, b/k and c/l are the intercepts of the plane with the x-axis, y-axis and z-axis respectively and h, k, l are by definition, integers.
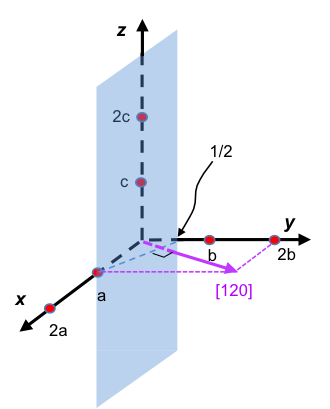
In the diagram above, the plane intercepts the x-axis, y-axis and z-axis at a, b/2 and ∞c respectively. Hence,
The variables h, k, l are called the Miller indices and are used to describe the orientation of planes via the notation (hkl).
The plane, in this case, is (120). If we draw a position vector that is perpendicular to the plane (depicted as the purple arrow in the diagram), we can describe the vector with the direction [120], which is consistent with the Miller index of the plane. Furthermore, the Miller index of a plane may contain negative numbers, e.g. (1 -2 0) which is denoted by .
Consider a crystal with monoclinic unit cells. Due to the periodic arrangement of lattice points, we can find many different planes intersecting the points. The diagram below depicts parallel planes with the middle one having the Miller index of (001) and the top plane of (00½). As whole numbers are preferred in the (hkl) notation, (00½) is rewritten as (001) by multiplying each of the three numbers by the smallest integer that will give whole numbers.
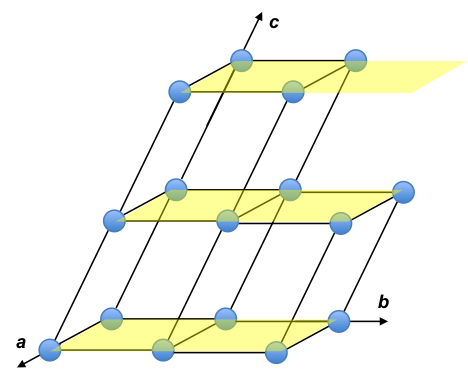
If we shift the origin from the far left lattice point of the bottom layer to the far left lattice point of the middle layer, the top plane becomes (001) and the bottom plane becomes . Furthermore, the parallel planes are equivalent by a rotation of the lattice and form a family of planes. In general, we denote the set of all planes that are equivalent to a particular reference plane (hkl) by the symmetry of the lattice as {hkl}. Therefore, we describe this family of planes as {001}. This example shows that the Miller notation does not require axes to be orthogonal to each other.

Question
Can we denote the family of planes in the above diagram as ?
Answer
Yes. However, the convention is to select the plane that is closest to the origin that has positive indices as the reference plane for the family. Hence, the notation {001} is preferred.
