Powder X-ray diffraction is a scientific method for determining the structure of materials. The diagram below shows the main components of a powder X-ray diffractometer.
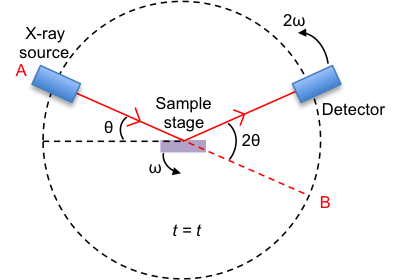
The substance to be analysed is placed on the sample stage. It is in its powder (or polycrystalline) form, which contains millions of grains of three-dimensional lattices that are randomly orientated in space (see figure II below). Therefore, every possible orientation of every set of lattice plane is present in the sample.

The position of the X-ray source is fixed, while the sample stage is rotated at an angular rate of ω, where ω = dθ/dt. The detector is rotated in the same direction as the sample stage but at an angular rate of 2ω.
Consider the sample stage being parallel to the line AB and the detector at B when t = 0. At t = t, the sample stage makes an angle θ with the incident X-ray vector, while the detector collects scattered or diffracted X-ray that makes an angle of 2θ with the incident X-ray. By convention, the angles of diffraction are recorded at 2θ instead of θ.

Question
Why does the detector rotate at a higher angular rate than the sample stage?
Answer
With reference to the above diagram depicting the diffractometer, the detector will always point along a line that is parallel to the sample stage if its angular rate of rotation is the same as that of the sample stage. It must rotate at a higher rate than ω for any meaningful detection. The rate 2ω is conventionally used.
If there are sufficient grains with lattice planes parallel to the sample stage at t = t (which is statistically possible due to the presence of millions of randomly orientated grains) and Bragg’s law is satisfied, a diffraction signal is recorded.
Let’s assume that figures III, IV, V show the orientation of three grains of a sample of polonium, which has a primitive cubic unit cell dimension of 337 pm, at time t = t where 2θ = 12.1o. If Mo X-ray of wavelength 71.0 pm were used, and that figures III, IV and V correspond to the family planes of {100}, {100} and {110} respectively , the only grain that has the required orientation to satisfy Bragg’s law is the one in figure III. This is validated by substituting all the relevant variables in eq13.
Figure IV does not satisfy Bragg’s equation, which requires θ1 = θ2 = θ, i.e. incident ray from the source and the scattered ray received by the detector must make the same angle with a lattice plane. Even though specular angles are observed in figure V, a (110) plane of polonium satisfies Bragg’s equation only if 2θ = 17.1o. This is because the interplanar distance of (110) is different from that of (100) and therefore causes scattered X-rays from adjacent lattice points of (110) planes to interfere destructively at 2θ = 12.1o.
Therefore, only one signal corresponding to the family planes of {100} is observed at 2θ = 12.1o. Using the same logic, signals corresponding to {110}, {111}, {200}, … are recorded at 2θ of 17.1o, 21.0o, 24.3o, …. Finally, a spectrum of intensity versus 2θ is generated by the diffractometer for analysis.

Question
Do the planes (010) and (001) for a primitive cubic system give the same diffraction signal as the (100) plane in powder X-ray diffraction?
Answer
Yes, as the grains are randomly distributed. Since the (010) and (001) planes for a primitive cubic unit cell are equivalent to the reference plane (100) by the symmetry of the lattice, the three planes belong to the same family of planes, denoted by {100}, i.e. the signal from {100} includes scattered X-rays from all these planes. For the purpose of unit cell identification, it is not necessary to distinguish the different planes within the same family of planes.
How do we identify the unit cell and determine its dimensions for an unknown sample using powder X-ray diffraction? Part of the solution requires the understanding of systematic absences, which is described in the next section.
