The interplanar distance is the perpendicular distance between two adjacent planes of a family of planes.
Consider a family of parallel planes {hkl} with the reference plane shown in the diagram below.

The interplanar distance, dhkl, is given by
Similarly, we have
For orthogonal axes, cos2α + cos2β + cos2γ = 1 (see below for proof),
Therefore, eq3 describes the interplanar distance for an orthorhombic unit cell. For a primitive cubic unit cell, a = b = c and eq3 becomes
The diagram below shows two parallel planes with Miller indices of (110) and (220).

The interplanar distance for (110), i.e. between the orange plane and the origin, is twice of that for (220). If we rewrite (220) as (n1 n1 n0), d110 = ndn1,n1,n0 where n = 2. In general, for parallel and equidistant planes,
where n ∈ . n is called the common factor between planes. Substituting eq5 in eq3 and eq4, we have:

Question
Show that cos2α + cos2β + cos2γ = 1 for orthogonal axes.
Answer
With reference to the diagram below,
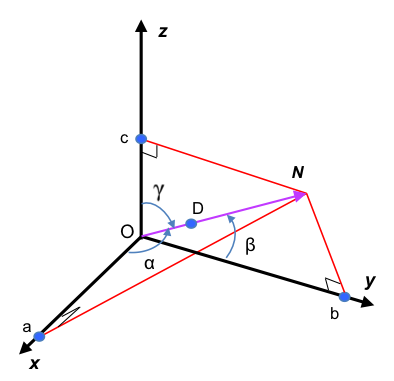
Since a2 + b2 + c2 = INI2
