The Ewald sphere is a mathematical construct that relates the geometry of the incident and scattered wave vectors to the reciprocal lattice.
Consider a crystal at A being irradiated by an incident wave vector s0, scattering a wave vector s that makes an angle 2θ with s0, thereby satisfying Bragg’s law (see diagram below).
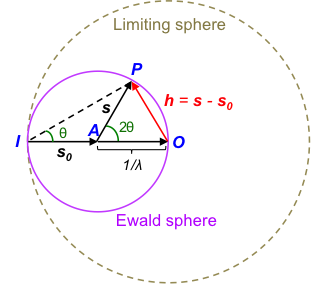
Since X-ray scattering is elastic, IsI = Is0I and the two wave vectors become radii of a sphere called the Ewald sphere. The vector OP is the reciprocal lattice vector (s – s0) that is denoted by h with the origin at O.
Since h = (s – s0), eq24 becomes
From eq11, . Substitute
and eq24f in eq24e, we have:
This means that IA = AO = AP = 1/λ. Therefore, to satisfy Bragg’s law that results in constructive interference of scattered X-rays, the head of the reciprocal lattice vector must lie on any point on the surface of the Ewald sphere. From eq24f and eq11,
Since -1 ≤ sinθ ≤ 1,
As the maximum magnitude of the reciprocal lattice vector is 2/λ, all reciprocal lattice vectors that potentially satisfy the Laue equations or Bragg’s law are enclosed in a sphere of radius known as the limiting sphere. The Ewald sphere is used to visualize different X-ray diffraction techniques including single crystal X-ray diffraction.
