Single crystal X-ray diffraction is an analytical technique to determine the structure of a single crystal.
Unlike the polycrystalline sample used in powder X-ray diffraction, a monocrystalline sample or single crystal does not have three-dimensional lattices that are randomly oriented in space. The sample has to be rotated in different directions so that scattered X-rays from all lattice planes satisfying Bragg’s law are recorded. This is accomplished by a single crystal X-ray diffractometer called the four circle diffractometer (see diagram below).
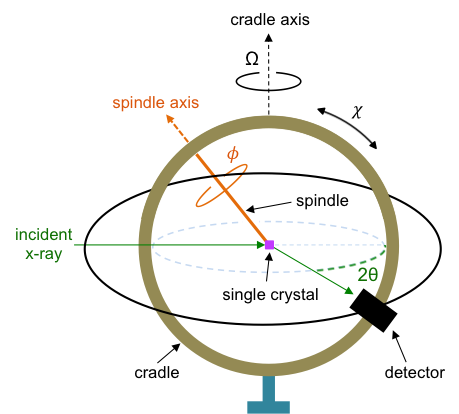
Crystal growth usually involves dissolving the chemical species to be analysed in a mixture of solvents, which evaporates over time and therefore allows the concentration of the solute to rise until crystallisation occurs. A single crystal of about 0.1-0.4 mm in all dimensions is then selected and mounted on the head of the spindle.
The single crystal is rotated through one of the four angles at each turn. The four angles are:
- 2θ, between the diffracted ray and the incident ray. This angle varies with the rotation of the detector in the equatorial plane that contains the incident and diffracted rays. 2θ = 0 when the detector is in the direction of the incident X-ray.
- Ω, defined by the rotation of the cradle around the cradle axis. Ω = 0 when the cradle is perpendicular to the incident X-ray.
- χ, between the spindle axis and the cradle axis. This angle varies with the rotation of the cradle in the clockwise or counter-clockwise direction. χ = 0 when the spindle axis is parallel to the cradle axis, at which the Ω and Φ rotations coincide.
- Φ, the angle of rotation of the spindle around the spindle axis. The zero position of Φ is defined with reference to the crystal orientation.
We can use the Ewald sphere to visualise various rotations with respect to the reciprocal lattice (see diagram below).
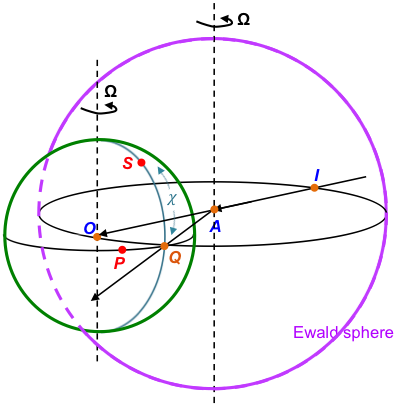
The single crystal at A is irradiated by an incident X-ray IA, scattering a wave vector that intersects the surface of the Ewald sphere at Q. Consider the case where Bragg’s law (or Laue equations) is satisfied, i.e. ∠OAQ = 2θ. Even though reciprocal lattice points spans across and beyond both spheres, we shall focus on those enclosed by the green sphere with the origin of the reciprocal lattice vector at O. As the single crystal at A rotates about the cradle axis, reciprocal lattice points formed by scattered X-rays from the crystal rotate about an axis at O that is parallel to the cradle axis (since O is the origin of the reciprocal lattice vector).
A reciprocal lattice point P therefore satisfies Bragg’s law when it is rotated by a certain value of Ω to Q. As this rotation corresponds to X-rays scattered by a particular lattice plane, the point P is assigned a (hkl) value after the rotation data is analysed by a computer. Similarly, a reciprocal lattice point S when rotated by an angle χ satisfies Bragg’s law when it reaches Q. In short, data is collected by the computer at each turn and analyses of systematic absences, electron densities and so on are carried out to give the structure of the sample.

