Change of basis

A change of basis is a method to convert vector coordinates with respect to one basis to coordinates with respect to another basis.

Consider a vector u with reference to orthogonal unit basis vectors x₁, x₂and x₃.

$\textbf{\textit{u}}=px_1+qx_2+rx_3\; \; \; \; \; \; \; (1)$

where p, q and r are the scalar components of the unit basis vectors x₁, x₂and x₃ respectively. Clearly,

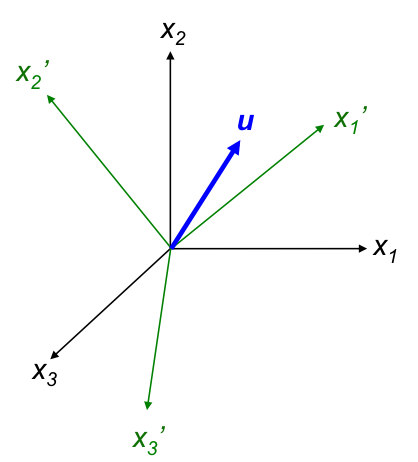
$p=\textbf{\textit{u}}\cdot x_1\; \; \; \; q=\textbf{\textit{u}}\cdot x_2\; \; \; \; r=\textbf{\textit{u}}\cdot x_3\; \; \; \; (2)$

If we define u with respect to another orthogonal reference frame with unit basis vectors x’₁, x’₂and x’₃ (see above diagram), we have:

$\textbf{\textit{u}}=p' x'_1+q'x'_2+r'x'_3\; \; \; \; (3)$

and

$p'=\textbf{\textit{u}}\cdot x'_1\; \; \; \; q'=\textbf{\textit{u}}\cdot x'_2\; \; \; \; r'=\textbf{\textit{u}}\cdot x'_3\; \; \; \; (4)$

To find the relationship between the two reference frames, we substitute eq1 in eq4 to give:

$p'=\left ( px_1+qx_2+rx_3 \right )\cdot x'_1=px_1\cdot x'_1+qx_2\cdot x'_1+rx_3\cdot x'_1\; \; \; \; \; \; \; (5)$

$q'=\left ( px_1+qx_2+rx_3 \right )\cdot x'_2=px_1\cdot x'_2+qx_2\cdot x'_2+rx_3\cdot x'_2\; \; \; \; \; \; \; (6)$

$r'=\left ( px_1+qx_2+rx_3 \right )\cdot x'_3=px_1\cdot x'_3+qx_2\cdot x'_3+rx_3\cdot x'_3\; \; \; \; \; \; \; (7)$

Since the dot product of two vectors gives a scalar, we can write eq5, eq6 and eq7 as:

$p'=a_{11}p+a_{12}q+a_{13}r$

$q'=a_{21}p+a_{22}q+a_{23}r$

$r'=a_{31}p+a_{32}q+a_{33}r$

which can be expressed in the following matrix equation:

$\begin{pmatrix} p'\\ q'\\ r' \end{pmatrix}=\begin{pmatrix} a_{11} &a_{12} &a_{13} \\ a_{21} & a_{22} &a_{23} \\ a_{31} &a_{32} & a_{33} \end{pmatrix}\begin{pmatrix} p\\ q\\ r \end{pmatrix}\; \; \; \; \; \; \; (8)$

where $a_{ij}=x'_i\cdot x_j=\left | x'_i \right |\left | x_j \right |cos\theta_{x'_i,x_j}=cos\theta _{x'_i,x_j}$ . The matrix containing a_ij is known as the change of basis matrix . We can rewrite eq8 as:

$u'_i=\sum_{j=1,2,3}a_{ij}u_j\; \; \; \; \; \; \; (9)$

where $u'_1=p',u'_2=q',u'_3=r'$ and $u_1=p,u_2=q,u_3=r$ . Eq9 is often written as a short form by omitting the summation symbol:

$u'_i=a_{ij}u_j\; \; \; \; \; \; \; (10)$

For example, the change of basis from the orthogonal basis x_j to the orthogonal basis x’_ias a rotation about the x₃-axis, where x₃coincides with x’₃ (x’₃= x₃ and is perpendicular to the plane of the page), is depicted as:

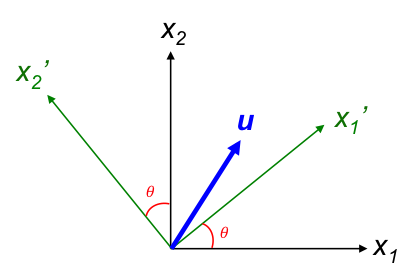
To determine the change of basis matrix, we have

$x'_1\cdot x_3=x'_3\cdot x_1=x'_2\cdot x_3=x'_3\cdot x_2=cos90^o=0$

$x'_3\cdot x_3=cos0^o=1$

$x'_1\cdot x_1=x'_2\cdot x_2=cos\theta$

$x'_1\cdot x_2=cos\left ( 90^o-\theta \right )=sin\theta$

$x'_2\cdot x_1=cos\left ( 90^o+\theta \right )=-sin\theta$

Therefore,

$a_{ij}=\begin{pmatrix} a_{11} & a_{12}&a_{13}\\ a_{21}& a_{22}&a_{23}\\ a_{31}& a_{32}& a_{33}\end{pmatrix}=\begin{pmatrix} x'_1\cdot x_1 & x'_1\cdot x_2&x'_1\cdot x_3\\ x'_2\cdot x_1&x'_2\cdot x_2 &x'_2\cdot x_3\\ x'_3\cdot x_1& x'_3\cdot x_2& x'_3\cdot x_3\end{pmatrix}=\begin{pmatrix} cos\theta &sin\theta &0 \\ -sin\theta & cos\theta &0 \\ 0 &0 &1 \end{pmatrix}\; \; \; \; \; \; \; (12)$

Consider again the vector u with reference to a coordinate system that is defined by the orthogonal unit basis vectors x₁, x₂and x₃ (see diagram below).

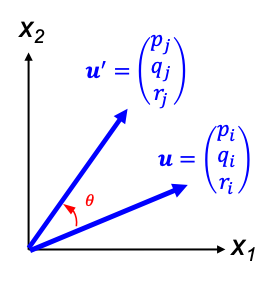
The rotation of u with respect to this fixed coordinate system is expressed as:

$\begin{pmatrix} p_j\\ q_j\\ r_j \end{pmatrix}=\begin{pmatrix} cos\theta &-sin\theta &0 \\ sin\theta & cos\theta &0 \\ 0 &0 & 1 \end{pmatrix}\begin{pmatrix} p_i\\ q_i\\ r_i \end{pmatrix}\; \; \; or\; \; \; \; \boldsymbol{\mathit{u'}}=R\boldsymbol{\mathit{u}}$

Compared to the change of basis of u that was described earlier, the rotation matrix R is the inverse of the change of basis matrix (similarly, a reflection matrix is the inverse of the change of basis matrix by a reflection). In other words, the rotation of u by θ can be perceived a change of basis, with the coordinate system rotated by –θ. This implies that we can analyse a problem in two ways.

Next article: Tensor and tensor transformation

Content page of tensors

Content page of advanced chemistry

Main content page