Constitutive relation: hypothesis 3

The third constitutive relation hypothesis states that the shear stress tensor is zero if the flow involves no shearing of the fluid-body.

A square matrix A is symmetric if a_ij = a_jifor all i and j, i.e. A = A^T, e.g.

$\begin{pmatrix} 1 &5 &-3 \\ 5 &8 &0 \\ -3 &0 &2 \end{pmatrix}$

A square matrix is anti-symmetric (or skew symmetric) if a_ij = –a_jifor all i and j, i.e. –A = A^T, e.g.

$\begin{pmatrix} 0 &-7 &3 \\ 7 &0 &-4 \\ -3 &4 &0 \end{pmatrix}$

If a_ij = –a_ji , the diagonal components of the matrix must all be zero.

In general, we can write a square matrix in the following form:

$A=\frac{1}{2}\left ( A+A^T \right )+\frac{1}{2}\left ( A-A^T \right )=B+C$

where B = (A + A^T)/2, C = (A – A^T)/2 and A^Tis the transpose of A.

Using the transpose identity of (X + Y)^T = X^T+ Y^T (which can be verified by substituting any matrix with any components into the equality), we can show that B is symmetric (B = B^T) and C is anti-symmetric (C = –C^T).

This means that a square matrix can be decomposed into a symmetric and an anti-symmetric component. From the previous section, $\frac{\partial u_k}{\partial x_l}$ is a second-order tensor that can be represented by a 3×3 matrix. Therefore,

$\frac{\partial u_k}{\partial x_l}=\left [ \frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}+\frac{\partial u_l}{\partial x_k}\right )+\frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}-\frac{\partial u_l}{\partial x_k}\right )\right ]\; \; \; \; \; \; \; (9)$

where $\frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}+\frac{\partial u_l}{\partial x_k}\right )$ is symmetric and $\frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}-\frac{\partial u_l}{\partial x_k}\right )$ is anti-symmetric.

Substitute eq9 in eq8,

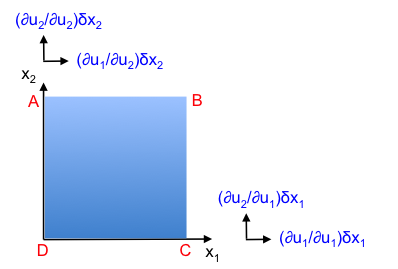
$\tau_{ij}=\alpha_{ijkl}\left [ \frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}+\frac{\partial u_l}{\partial x_k}\right )+\frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}-\frac{\partial u_l}{\partial x_k}\right )\right ]\; \; \; \; \; \; \; (10)$

Consider a two-dimensional body of fluid ABCD as depicted in the above diagram. The term $\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1}\right )$ tends to shear the fluid. If we consider the rotation of the fluid in the clockwise direction, the term $\left ( \frac{\partial u_1}{\partial x_2}-\frac{\partial u_2}{\partial x_1}\right )$ tends to rotate the fluid. This means that $\frac{\partial u_k}{\partial x_l}$ in eq9 can be non-zero even if the shear component $\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1}\right )$ is zero, as the rotation component $\left ( \frac{\partial u_1}{\partial x_2}-\frac{\partial u_2}{\partial x_1}\right )$ is non-zero. However, hypothesis 3 states that the shear stress tensor τ_ij in eq10 is zero if the flow involves no shearing of the fluid-body. To satisfy hypothesis 3, eq10 becomes:

$\tau_{ij}=\beta_{ijkl}\: \frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}+\frac{\partial u_l}{\partial x_k}\right )\; \; \; \; \; \; \; (11)$

β_ijkl, which is composed of eighty-one components, characterizes the properties of the fluid. Since $\frac{1}{2}\left ( \frac{\partial u_k}{\partial x_l}+\frac{\partial u_l}{\partial x_k}\right )$ is symmetric, and β_ijklconsists of scalar components, τ_ijis also symmetric.

Constitutive relation: hypothesis 3

next article: hypothesis 4

Previous article: hypothesis 2

Content page of constitutive relation

Content page of advanced chemistry

Main content page