The second hypothesis formulating the constitutive relation for an incompressible, viscous Newtonian fluid states that the shear stress tensor is a linear function of the deformation tensor.
Consider a shear stress τ that is coplanar to a cross section of a Newtonian fluid ABCD as shown in the diagram below.
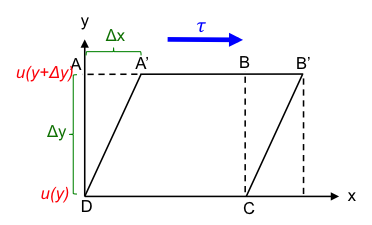
The fluid is continuously deformed by the force with different layers of the fluid having different velocities, u(y) at point D and u(y + Δy) at point A. At time t, the body of fluid moves from ABCD to A’B’CD. Let’s define the shear strain in the fluid as where
If Δy → 0,
If t is small,
We call the shear strain rate and
the velocity gradient of the fluid. Clearly, the greater the shear stress applied, the higher the value of the shear strain rate, i.e.:
where μ is the constant of proportionality, which is attributed to the resistance of the fluid to the shear stress. We call this resistance, the viscosity of the fluid. Substituting eq5 in eq6, we have the Newton’s law of viscosity,
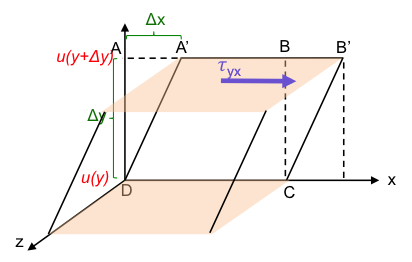
When extended to three dimensions (see above diagram), eq7 becomes:
From eq4 of the previous article, shear stress is a second-order tensor with nine components τij . Hence, the general form of eq7 is:
where for a Cartesian system, i = 1, 2, 3, j = 1, 2, 3 and x1 = x, x2 = y, x3 = z.
can therefore be expressed as a second-order tensor (deformation tensor) of nine components. Since each of the nine components of τij is linearly proportional to each of the nine components of
, there are a total of 92 = 81 proportionality constants. In other words,
where is a fourth-order tensor of eighty one components, which can be representation by a 3x3x3x3 matrix for a Cartesian system. This satisfies hypothesis 2.
The fourth-order tensor, which is composed of the proportionality constants, characterises the properties of the fluid.