Isotropic tensors

An isotropic Cartesian tensor is one where its components are identical in any orthogonal Cartesian system.

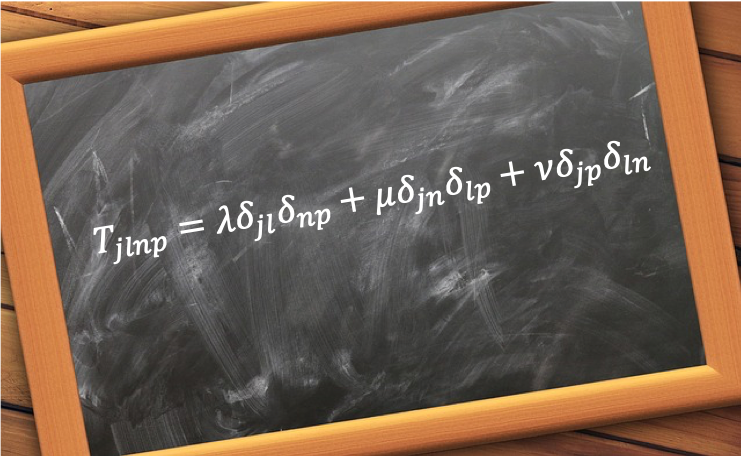
An isotropic property is one that is independent of direction, e.g. thermal expansion of a solid, and therefore has a quantity that is independent of the reference frame. An isotropic property can therefore be described by a Cartesian tensor like $T'_{j_1j_2...j_n}$ in eq15.

To evaluate the properties of an isotropic tensor, we begin by considering a generic fourth-order tensor $T_{jlnp}$ , whose transformation is expressed by eq14:

$T'_{ikmo}=a_{ij}a_{kl}a_{mn}a_{op}T_{jlnp}\; \; \; \; \; \; \; (16)$

Since j, l, n and p, each of which ranges from 1 to 3, the 81 components of $T'_{ikmo}$ are classified in four groups as follows:

Components with four equal subscripts, i.e. $T'_{1111}$ , $T'_{2222}$ and $T'_{3333}$ .
Components with three equal subscripts, e.g. $T'_{1211}$ , $T'_{2223}$ , etc.
Components with two different pairs of equal subscripts, e.g. $T'_{1212}$ , $T'_{3322}$ , $T'_{1331}$ , etc.
Components with one pair of equal subscripts, e.g. $T'_{1213}$ , $T'_{2213}$ , etc.

Next, consider the transformation of $T_{jlnp}$ to $T'_{ikmo}$ as a rotation about the x₃-axis of $\theta=180^o$ where x₃coincides with x’₃(x’₃is equal to x₃and is perpendicular to the plane of the page). From eq12, the transformation matrix is:

$a_{ij}\: or\: a_{kl}\: or\: a_{mn}\: or\: a_{op}=\begin{pmatrix} cos\theta &sin\theta &0 \\ -sin\theta &cos\theta &0 \\ 0 &0 &1 \end{pmatrix}=\begin{pmatrix} -1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &1 \end{pmatrix}$

Therefore, $a_{11}=a_{22}=-1$ and $a_{33}=1$ , with the rest of the components of the transformation matrix equal to zero. From eq16, a component of group 2 of the above classification is:

$T'_{1113}=a_{1j}a_{1l}a_{1n}a_{3p}T_{jlnp}=a_{11}a_{11}a_{11}a_{31}T_{1111}+a_{11}a_{11}a_{11}a_{32}T_{1112}$

$+a_{11}a_{11}a_{11}a_{33}T_{1113}+...\; \; \; \; \; \; \; (17)$

Substituting $a_{11}=a_{22}=-1$ , $a_{33}=1$ and $a_{i\neq j}=0$ in eq17, we have:

$T'_{1113}=-T_{1113}\; \; \; \; \; \; \; (18)$

If $T_{jlnp}$ is an isotropic tensor, $T'_{1113}=T_{1113}$ (since an isotropic Cartesian tensor is one where its components are identical in any orthogonal Cartesian system). Hence, the only way to satisfy eq18 is for $T'_{1113}=T_{1113}=0$ . Otherwise, the value of $T'_{1113}$ varies with the value of $T_{1113}$ , e.g. when $T_{1113}=-7$ , $T'_{1113}=7$ .

Another component of group 2 of the above classification is $T'_{1211}$ where after expanding and substituting with $a_{11}=a_{22}=-1$ , $a_{33}=1$ and $a_{i\neq j}=0$ ,

$T'_{1211}=T_{1211}\; \; \; \; \; \; \; (20)$

Eq20 shows that $T'_{1211}=T_{1211}$ but does not indicate the value of either component. If the rotation is instead made about the x₂-axis at $\theta=180^o$ , the transformation matrix is:

$\begin{pmatrix} cos\theta & 0 &sin\theta \\ 0 & 1 &0 \\ -sin\theta &0 &cos\theta \end{pmatrix}=\begin{pmatrix} -1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &-1 \end{pmatrix}$

We have $a_{11}=a_{33}=-1,a_{22}=1$ , and $a_{i\neq j}=0$ , giving $T'_{1211}=-T_{1211}$ . If $T_{jlnp}$ is an isotropic tensor,

$T'_{1211}=T_{1211}=0\; \; \; \; \; \; \; (22)$

Repeating the above steps and assuming that $T_{jlnp}$ is an isotropic tensor, we find that all the components of $T'_{ikmo}$ in group 2 and group 4 are zero, which means that all the components of $T_{jlnp}$ in group 2 and group 4 are zero.

We shall now analyse the components of group 1 by a rotation about the x₃-axis at $\theta=90^o$ with the transformation matrix:

$\begin{pmatrix} cos\theta &sin\theta &0 \\ -sin\theta &cos\theta &0 \\ 0 &0 &1 \end{pmatrix}=\begin{pmatrix} 0 &1 &0 \\ -1 &0 &0 \\ 0 &0 &1 \end{pmatrix}$

We have $T'_{1111}=T_{2222},T'_{2222}=T_{1111},T'_{3333}=T_{3333}$ .

A rotation about the x₂-axis at $\theta=90^o$ involves the transformation matrix:

$\begin{pmatrix} cos\theta & 0&sin\theta \\ 0 &1 &0 \\ -sin\theta &0 & cos\theta\end{pmatrix}=\begin{pmatrix} 0 &0 &1 \\ 0 &1 &0 \\ -1 &0 &0 \end{pmatrix}$

and gives $T'_{1111}=T_{3333},T'_{2222}=T_{2222},T'_{3333}=T_{1111}$ .

Comparing the six equations $T'_{1111}=T_{2222},T'_{2222}=T_{1111},T'_{3333}=T_{3333}$ and $T'_{1111}=T_{3333},T'_{2222}=T_{2222},T'_{3333}=T_{1111}$ , all the components of $T'_{ikmo}$ in group 1 are equal to one another, which means that all the components of $T_{jlnp}$ in group 1 are equal to one another.

Finally, let’s look at the components in group 3. Under a rotation about the x₃-axis at $\theta=90^o$ , we have $T'_{1122}=T_{2211},T'_{2233}=T_{1133},T'_{3311}=T_{3322}$ .

A rotation about the x₂-axis at $\theta=90^o$ gives $T'_{1122}=T_{3322},T'_{2233}=T_{2211},T'_{3311}=T_{1133}$ .

Comparing the six equations $T'_{1122}=T_{2211},T'_{2233}=T_{1133},T'_{3311}=T_{3322}$ and $T'_{1122}=T_{3322},T'_{2233}=T_{2211},T'_{3311}=T_{1133}$ , components in group 3 of $T'_{ikmo}$ (which is equal to the components in group 3 of $T_{jlnp}$ ) with i = k and m = o are equal to one another. Repeating the above steps, we can show that components in group 3 with i = m and k = o are equal to one another and those with i = o and k = m are equal to one another.

Therefore, if $T_{jlnp}$ is an isotropic tensor:

i) components of $T'_{ikmo}$ with i = k = m = o are equal and therefore $T_{jlnp}$ with j = l = n = p are equal

ii) components of $T'_{ikmo}$ with i = k ≠ m = o are equal and therefore $T_{jlnp}$ with j = l ≠ n = p are equal

iii) components of $T'_{ikmo}$ with i = m ≠ k = o are equal and therefore $T_{jlnp}$ with j = n ≠ l = p are equal

iv) components of $T'_{ikmo}$ with i = o ≠ k = m are equal and therefore $T_{jlnp}$ with j = p ≠ l = n are equal

v) all other components not mentioned are equal to zero

Note that components of parts ii, iii and iv belong to group3 of the isotropic tensor. Now, consider a case of $T_{jlnp}$ where components of $T_{jlnp}$ in iii and iv are set to zero ( $T_{jlnp}$ is still an isotropic tensor but with more components equal to zero). A rotation about the x₃-axis at $\theta=45^o$ gives the transformation matrix:

$\begin{pmatrix} cos\theta &sin\theta &0 \\ -sin\theta &cos\theta &0 \\ 0 & 0 &1 \end{pmatrix}=\begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0\\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} &0 \\ 0 &0 &1 \end{pmatrix}$

Since components in part iii and part iv are set to zero and the conditions of part v applies, we have $T'_{1111}=\frac{1}{4}T_{1111}+\frac{1}{4}T_{1122}+\frac{1}{4}T_{2211}+\frac{1}{4}T_{2222}$ . Furthermore, part i states that $T_{1111}=T_{2222}$ and part ii states that $T_{1122}=T_{2211}$ . So,

$T'_{1111}=\frac{1}{2}\left ( T_{1111}+T_{1122}\right )\; \; \; \; \; \; \; (23)$

If $T_{jlnp}$ is an isotropic tensor, $T'_{1111}=T_{1111}$ and therefore, $T_{1111}=T_{1122}$ . This means that all non-zero components of this particular $T_{jlnp}$ have the same value, say, λ, where:

$T_{jlnp}=\lambda\delta_{jl}\delta_{np}\; \; \; \; \; \; \; (24)$

where $\delta_{jl}$ and $\delta_{np}$ are Kronecker deltas.

Using the same logic by considering the cases of $T_{jlnp}$ where components of $T_{jlnp}$ in part ii and part iv are set to zero and where components of $T_{jlnp}$ in part ii and part iii are set to zero, we have:

$T_{jlnp}=\mu\delta_{jn}\delta_{lp}\; \; \; \; \; \; \; (25)$

and

$T_{jlnp}=\nu\delta_{jp}\delta_{ln}\; \; \; \; \; \; \; (26)$

respectively.

Therefore, we can write the general form of the fourth-order isotropic tensor as:

$T_{jlnp}=\lambda\delta_{jl}\delta_{np}+\mu\delta_{jn}\delta_{lp}+\nu\delta_{jp}\delta_{ln}\; \; \; \; \; \; \; (27)$

Question

Show that $T_{jlnp}$ in eq27 continues to satisfy parts i to v, all of which are needed to define a fourth-order isotropic tensor.

Answer

In eq27,

i) the components of $T_{jlnp}$ with j = l = n = p have values of $\lambda+\mu+\nu$ and are therefore still equal to one another;

ii) the components of $T_{jlnp}$ with j = l ≠ n = p have values of $\lambda$ and are therefore still equal to one another;

iii) the components of $T_{jlnp}$ with j = n ≠ l = p have values of $\mu$ and are therefore still equal to one another;

iv) the components of $T_{jlnp}$ with j = p ≠ l = n have values of $\nu$ and are therefore still equal to one another;

v) all other components not mentioned are equal to zero.

Therefore, the general form of the fourth-order isotropic tensor is valid.

Question

Answer

previous article: tensor and tensor transformation

Content page of tensors

Content page of advanced chemistry

Main content page