Why is initial rate proportional to 1/t?

The ‘initial rate proportional to 1/t’ concept is applicable to a chemical kinetics experiment that has the initial concentration of a reactant varied but the measured amount of a product fixed. One such experiment is the decomposition of hydrogen peroxide over a platinum catalyst, while another is the iodine clock. For the decomposition experiment, we have:

$2H_2O_2(aq)\rightleftharpoons2H_2O(l)+O_2(g)$

Using various initial concentrations of H₂O₂, different times taken to collect a fixed volume of oxygen are recorded. The diagram below illustrates the setup, where the fixed volume of oxygen produced under constant temperature is measured by a fixed change in pressure of the constant-volume system.

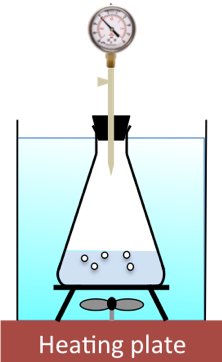
Since the reaction is very slow, we assume that the initial concentration of H₂O₂ for each experiment remains relatively unchanged for the volume of oxygen generated (the change in pressure of the system can be fixed at an amount that does not exceed three minutes to occur). Using eq10, and assuming gases behave ideally, we can write

$initial\, rate=\frac{d[O_2]}{dt}=\frac{\Delta (n_{O_2}/V)}{\Delta t}=\frac{\Delta p}{RT\Delta t}\; \; \; \; \; \; \;\; 27$

To produce a fixed volume of oxygen, the change in amount of oxygen, and hence the change in pressure of the system, is constant regardless of the concentration of H₂O₂ used. Thus,

$initial\, rate=C\frac{1}{\Delta t}\; \; \; \; \; \; \; \; 28$

where C is a constant and is equal to $\frac{\Delta p}{RT}$ .

This answers the question of why initial rate is proportional to 1/t.

To develop an equation that that allows us to further analyse the decomposition reaction, we propose the following rate law:

$initial\, rate=k[H_2O_2]_0^{\;\: i}\; \; \; \; \; \; \; \; 29$

where [H₂O₂]₀is the initial concentration of H₂O₂.

Taking the natural logarithm for both sides of eq28 and eq29, we have

$ln(initial\, rate)=ln\frac{1}{\Delta t}+ln\frac{\Delta p}{RT}\; \; \; \; \; \; \; \; 30$

and

$ln(initial\, rate)=iln[H_2O_2]_0+lnk\; \; \; \; \; \; \; \; 31$

Substitute eq31 in eq30

$ln\frac{1}{\Delta t}=iln[H_2O_2]_0+ln\frac{k}{\Delta p/RT}\; \; \; \; \; \; \; \; 32$

Therefore, using the time measurements for the fixed change in pressure to occur for different initial concentrations of H₂O₂, a plot of $ln\frac{1}{\Delta t}$ versus $ln[H_2O_2]_0$ gives a gradient of the order of the reaction, i, and a vertical intercept of $ln\frac{k}{\Delta p/RT}$ where k is the rate constant.

Question

Eq32 is derived using the rate equation $\frac{d[O_2]}{dt}=k[H_2O_2]_0^{\; \, i}$ . What if we define the rate equation as $-\frac{1}{2}\frac{d[H_2O_2]}{dt}=k_1[H_2O_2]_0^{\; \, i}$ ?

Answer

$-\frac{1}{2}\frac{\Delta n_{H_2O_2}/V_{H_2O_2}}{\Delta t}=k_1[H_2O_2]_0^{\: \, i}$

$ln\left ( -\frac{1}{2}\frac{\Delta n_{H_2O_2}}{V_{H_2O_2}} \right )+ln\frac{1}{\Delta t}=lnk_1+iln[H_2O_2]_0$

$ln\frac{1}{\Delta t}=iln[H_2O_2]_0+ln\left ( \frac{k_1}{-\Delta n_{H_2O_2}/2V_{H_2O_2}} \right )\; \; \; \; \; \; \; \; 33$

To produce a fixed volume of oxygen, the change in amount of H₂O₂, $\Delta n_{H_2O_2}$ , is a constant value regardless of the initial amounts of H₂O₂. For example, to produce 1 mole of oxygen, the change in amount of H₂O₂ is always -2 moles irrespective of how many moles of H₂O₂ there are to begin with. Furthermore, the same volume of H₂O₂is used as we vary [H₂O₂]. So, the 2^nd term on RHS of eq33 is a constant, which makes eq33, like eq32, a linear function.

Comparing eq33 with eq32,

$k_1=-\frac{\Delta n_{H_2O_2}RT}{2V_{H_2O_2}\Delta p}k$

Why is initial rate proportional to 1/t?

Question

Answer

Next article: Isolation method

Previous article: Initial rate method

Content page of intermediate chemical kinetics

Content page of intermediate chemistry

Main content page

Leave a Reply Cancel reply