The Aufbau principle (building up principle) states that an atom in the ground state has electrons filling its orbitals in the order of increasing energy. It was proposed by Niels Bohr and Wolfgang Pauli in the 1920s and is based on the observation that the lower the energy of a system is, the more stable it is.

Specifically, the principle adopts the rule, which was first suggested by Charles Janet in 1928, in his attempt to construct a version of the periodic table. It was later adopted by Erwin Madelung in 1936, as a rule on how atomic sub-shells are filled.
The empirical rule states that electrons fill sub-shells in the order of increasing value of where
is the principal quantum number and
is the angular quantum number. It further mentions that electrons fill sub-shells in the order of increasing value of
for sub-shells with identical values of
. For example,
| Subshell | Order | |||
|
1s |
1 | 0 | 1 | 1 |
|
2s |
2 | 0 | 2 | 2 |
|
2p |
2 | 1 | 3 | 3 |
| 3s | 3 | 0 | 3 |
4 |
| 3p | 3 | 1 | 4 |
5 |
| 3d | 3 | 2 | 5 |
7 |
| 4s | 4 | 0 | 4 |
6 |

The order of fill is represented by the diagram above. So, the ground state electron configuration (distribution of electrons) for calcium is 1s2 2s2 2p6 3s2 3p6 4s2 or [Ar]4s2, where [Ar] is the electron configuration of argon. The Aufbau principle works well for elements with atomic number but must be applied with a better understanding of orbital energy and electron repulsion for
.
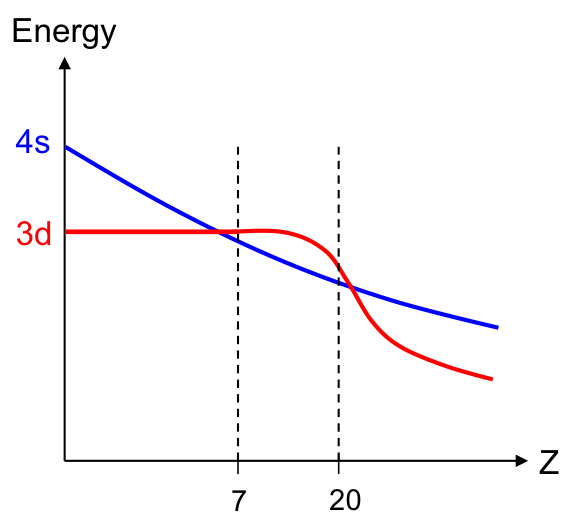
For elements with Z between 1 and 6, calculations show that the energy of the 4s sub-shell is higher than the 3d sub-shell (see diagram above). For Z between 7 and 20, the reverse is true, as a result of the interplay between increasing nuclear charge and increasing electron repulsion. The relative energy of the s and d sub-shells again changes for , where the 3d sub-shell has a lower energy than the 4s sub-shell. This is because electrons in 3d orbitals do not shield each other well from nuclear forces, leading to the lowering of their energies.
With that in mind, one may conclude that the electron configurations of scandium and titanium are [Ar]3d3 and [Ar]3d4 respectively. However, they are [Ar]3d14s2 and [Ar]3d24s2. Numerical solutions of the Schrodinger equation for scandium and titanium not only show that the 3d orbitals have lower energies than the 4s orbitals, but also reveal that the 3d orbitals are smaller in size compared to the 4s orbitals. Electrons occupying 3d orbitals therefore experience greater repulsions than electrons residing in 4s orbitals, with the order of increasing repulsion being:
where V is the potential energy due to repulsion.
To determine the stability of an atom in the ground state, we need to consider the net effect of the relative energies of 4s/3d orbitals and the repulsion of electrons. In fact, calculations for the overall energies of scandium are as follows:
Consequently, when a transition metal undergoes ionisation, the electron is removed from the 4s orbital rather than the 3d sub-shell. Despite 3d being lower in energy than 4s for the first row of transition metals, the rule applies. However, the rule breaks down for chromium and copper, where the ground state electronic configuration of chromium is [Ar]3d54s1 instead of [Ar]3d44s2 and that of copper is [Ar]3d104s1 instead of [Ar]3d94s2. This is attributed to Hund’s rule.
