The Born interpretation

The Born interpretation states that the probability of finding an electron of a certain quantum state around a point is proportional to the square of the modulus of the electron’s wave function $\left | \psi \right |^2$ , which is called the probability density. It was proposed by Max Born, a german Physicist, in 1926.

In developing the concept, Born drew a parallel between the probability of finding a particle in a region of space and the intensity of a classical wave, which is proportional to the square of the wave’s amplitude.

Question

Using Hooke’s law, F = –kx, show that the intensity of a wave is proportional to the square of its amplitude.

Answer

Substituting Hooke’s law in dE = –Fdx, we have dE = kxdx (where E is energy). Integrating the simple harmonic motion over a maximum amplitude A,

$E=\int_{0}^{A}kxdx=\frac{1}{2}kA^2$

Since intensity I is defined as $\frac{energy}{time\times area}$ , we have $I\propto E\propto A^2$ for an electromagnetic radiation falling on a particular area of a material over a certain duration.

Mathematically, the Born interpretation is:

$\int \left | \psi \right |^2d\tau$

or $\int \left | \psi \right |^2d\tau=1$ to ensure that the sum of individual probabilities of locating an electron over all space is normalised to one. The wave function of an electron is a complex quantity and therefore the above equation can be written as:

$\int \psi^*\psi d\tau$

where $\psi^*$ is the complex conjugate of $\psi$ .

Question

Why is the wave function a complex quantity? Show that $\psi^*\psi=\left | \psi \right |^2$ .

Answer

Some differential equations are easier to solve when the function is in the complex form. This happens to be the case for the Schrodinger equation. However, only the real component is used when values of the function are compared with experimental data.

Let $\psi=a+ib$ . So $\left | \psi \right |=\sqrt{a^2+b^2}\; \; \Rightarrow \; \; \left | \psi \right |^2=a^2+b^2$ .

$\psi^*\psi=(a-ib)(a+ib)=a^2+b^2$

Therefore, $\psi^*\psi=\left | \psi \right |^2$ .

In the previous article, we mentioned that Schrodinger did not have a convincing physical interpretation of the wave function ψ, other than it being a wave equation of an electron in the atom. With the Born interpretation, the electron probability density function $\left | \psi \right |^2$ for a unique combination of the three quantum numbers $n$ , $l$ and $m_l$ , mathematically describes an atomic orbital. When we plot the probability functions using a mathematical software, we obtain the following shapes:

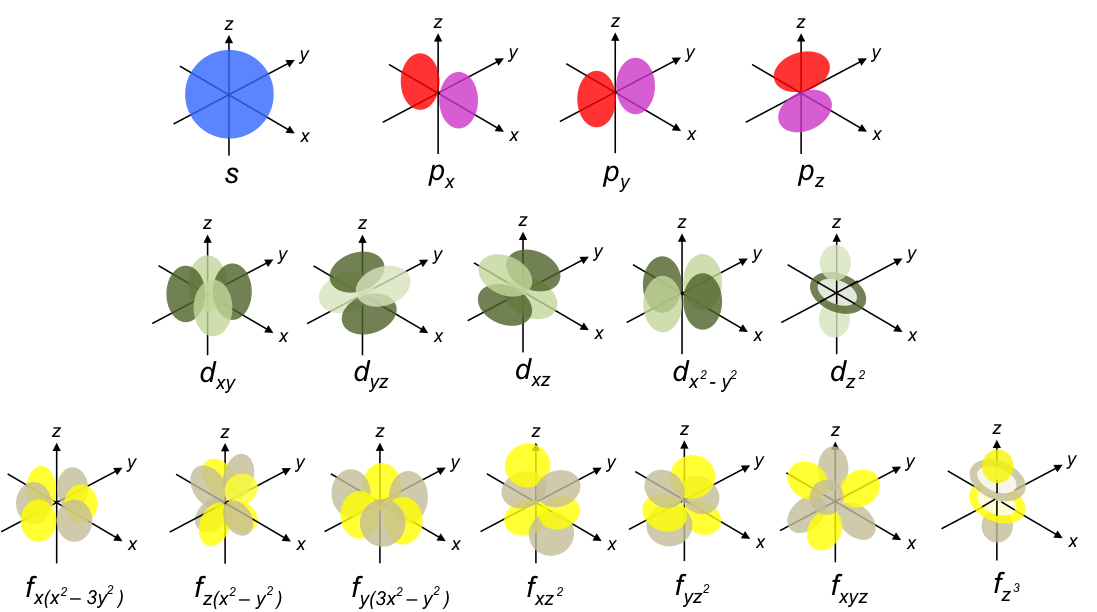
These are the orbitals of a hydrogen atom.

The Born interpretation

Question

Answer

Question

Answer

Next article: Electron spin

Previous article: Schrodinger equation

Content page of intermediate quantum chemistry

Content page of intermediate chemistry

Main content page

Leave a Reply Cancel reply