Electron spin

Ever since scientists recorded the first hydrogen emission spectrum, they produced many significant findings, including the Balmer and Lyman series, the Rydberg formula and the Bohr model. However, when researchers scrutinised the spectrum under magnification, they discovered that the emission line from n = 2 to n = 1 consisted of two lines (see diagram below).

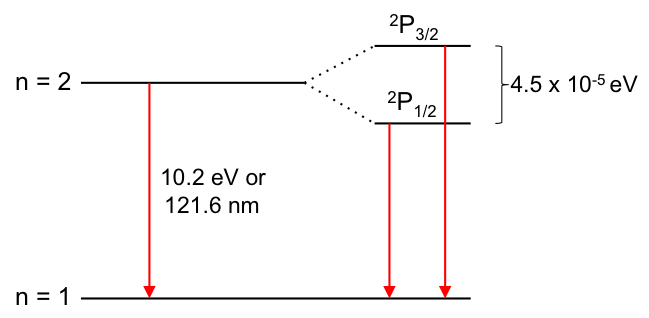
This splitting of emission lines is called the hydrogen fine structure. Many attempts were made to explain this phenomenon without success. At around 1924, Wolfgang Pauli, an Austrian physicist, and two other scientists (George Uhlenbeck and Samuel Goudsmit, both Dutch scientists), separately proposed that an electron possesses an intrinsic property called spin. Even though the spin of an electron is strictly a quantum mechanical property, it is possible to shed light on the concept using classical electromagnetism, where the electron is spinning on its own axis, while orbiting around the nucleus.

According to the classical model, a flow of charges generates a magnetic field, whose direction is given by the right-hand rule. An electron orbiting in a clockwise direction (when viewed from the top) around the nucleus of an atom therefore possesses a magnetic (orbital) dipole moment $\mu_l$ (see diagram below).

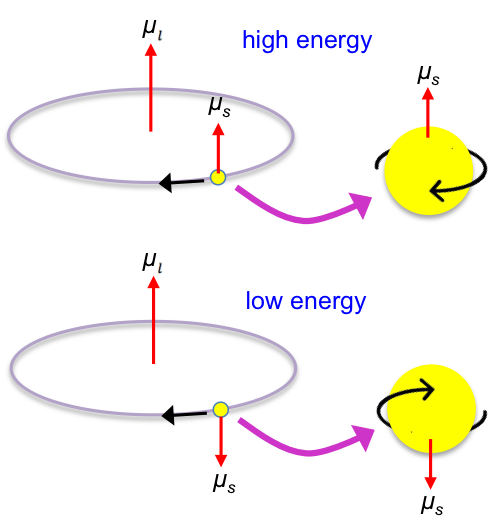
The electron spinning on its own axis in a clockwise direction has another magnetic (spin) dipole moment $\mu_s$ , because a spinning charge produces an effective current loop. Since the two dipole moments are vectors, they interact with each other to give an effective dipole moment. This ‘spin moment’-‘orbital field’ interaction is called spin-orbit coupling. If the allowed spin orientations are such that the magnetic spin dipole moments are either parallel or anti-parallel to the magnetic orbital dipole moment, the spin-orbit couplings will result in two quantum states of different energies.

Question

What is a magnetic dipole moment?

Answer

According to classical electromagnetic theory, a moving charge generates a magnetic field, which implies the presence of north and south magnetic poles called a magnetic dipole. The magnetic dipole moment is a measure of the strength and orientation of a magnetic dipole, i.e. a vector.

This is the reason why an electron, when excited to the n = 2 shell of the hydrogen atom, has one of two possible states (energy levels), namely ²P_3/2 and ²P_1/2. When the electron relaxes back to the n = 1 shell, one of two emission lines is observed, depending on whether the electron was initially promoted to the upper or lower state. The concept of electron spin and quantised spin orientations are validated by the Stern-Gerlach experiment, where a beam of silver atoms is directed through a magnetic field gradient.

In solving the Schrodinger equation for the hydrogen atom, the quantum number $l$ is attributed to the angular momentum of the electron as it orbits the nucleus. Since a particle possesses angular momentum, whether orbiting or spinning, a spinning electron has spin angular momentum. Furthermore, we know from the solution of Schrodinger’s equation that each value of $l$ (a vector) is associated with orientations of the magnetic number $m_l$ , where $m_l=-l,-l+1...0...l-1,l$ . With that, Pauli proposed a fourth quantum number $m_s$ , the spin magnetic number, to fully describe the quantum state of a system. Like $m_l$ , $m_s=-s,-s+1...0...s-1,s$ . The value of $s$ (another vector) was later experimentally determined to be $\frac{1}{2}$ . Therefore, $s$ has two possible orientations of $m_s=-\frac{1}{2}\; or\; +\frac{1}{2}$ .

Question

Shouldn’t the n = 1 shell split into two energy levels too?

Answer

The explanation above provides a qualitative picture of spin-orbit coupling. Mathematically, the spin-orbit interaction energy is computed using the formula:

$E=\frac{1}{2}hcA[j(j+1)-l(l+1)-s(s+1)]$

where h, c and A are constants, and j is the total angular momentum quantum number (i.e. the vector sum of $l$ and $s$ ). For the hydrogen atom, $j=l+s$ and $j=\left | l-s \right |$ .

According to the solution of the Schrodinger equation, when $n=1$ , we have $l=0$ , which makes j = s. Substituting these values in the above equation, we have a single value of E = 0. This means that there is no effect of spin-orbit coupling on the quantum state of n = 1. Using the same logic, we find that the quantum state for $n=2,l=1$ gives two values of E of $\frac{1}{2}hcA$ and $-\frac{1}{2}hcA$ , which when added to the energy of the quantum state of “ $n=2,l=1$ “, results in the states ²P_3/2 and ²P_1/2.