Spectral decomposition of an operator

The spectral decomposition (also known as eigendecomposition or diagonalisation) of an operator is the transformation of an operator in a given basis to one in another basis, such that the resultant operator is represented by a diagonal matrix.

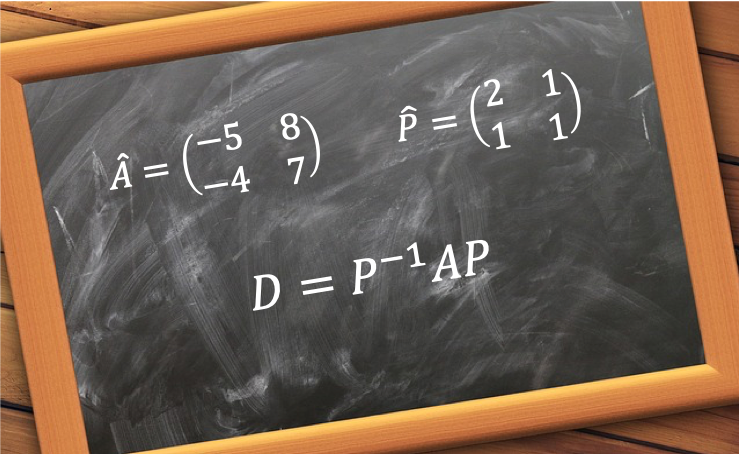
There are 2 main reasons for diagonalising an operator, especially a Hermitian operator. One is to find its eigenvalues and the other is to convert it into a form that is easier to multiply with.

Question

What is a spectrum with respect to linear algebra?

Answer

A spectrum is a collection of all eigenvalues of a matrix. If the matrix represents an operator, its spectral decomposition transforms it to a diagonal matrix with the eigenvalues as its diagonal elements.

Consider an operator with a complete set of orthonormal eigenvectors $\{\boldsymbol{\mathit{e_i}}\}$ that is represented by the eigenvalue equation $\hat{O}\vert\boldsymbol{\mathit{e_i}}\rangle=o_i\vert\boldsymbol{\mathit{e_i}}\rangle$ , where $i\in \mathbb{N}$ and $o_i$ are eigenvalues of $\hat{O}$ . Since the eigenvectors form a complete set, any vector $\boldsymbol{\mathit{u}}$ can be written as a linear combination of the basis eigenvectors:

$\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}c_i\vert\boldsymbol{\mathit{e_i}}\rangle \; \; \; \; \; \; \; \; 28$

where $c_i$ is the coefficient of the basis eigenvector.

Letting $\hat{O}$ act on eq28, $\hat{O}\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}c_io_i\vert\boldsymbol{\mathit{e_i}}\rangle$ . As we have a complete set of orthonormal eigenvectors, $\langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle=c_i$ and $\hat{O}\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}\langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle o_i\vert\boldsymbol{\mathit{e_i}}\rangle$ . Furthermore, $\langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle$ is a scalar and matrix multiplication is associative. Therefore,

$\hat{O}\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}o_i\vert\boldsymbol{\mathit{e_i}}\rangle\langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle =\left$\sum_{i=1}^{N}o_i\vert\boldsymbol{\mathit{e_i}}\rangle\langle\boldsymbol{\mathit{e_i}}\vert\right$\vert\boldsymbol{\mathit{u}}\rangle\; \; \; \; \; \; \; \; 29$

and

$\hat{O}=\sum_{i=1}^{N}o_i\vert\boldsymbol{\mathit{e_i}}\rangle\langle\boldsymbol{\mathit{e_i}}\vert\; \; \; \; \; \; \; \; 30$

We call eq30 the spectral decomposition of $\hat{O}$ .

Question

Show that $\hat{O}$ in eq30, where $N=3$ , is represented by a diagonal matrix.

Answer

$\hat{O}=o_1 \begin{pmatrix} 1\\ 0\\0 \end{pmatrix} \begin{pmatrix} 1 &0 &0 \end{pmatrix}+o_2 \begin{pmatrix} 0\\ 1\\0 \end{pmatrix} \begin{pmatrix} 0 &1 &0 \end{pmatrix}+o_3 \begin{pmatrix} 0\\ 0\\1 \end{pmatrix} \begin{pmatrix} 0 &0 &1 \end{pmatrix}$

$\hat{O}=o_1 \begin{pmatrix} 1 &0 &0 \\ 0 &0 &0 \\ 0 &0 &0 \end{pmatrix}+o_2 \begin{pmatrix} 0 &0 &0 \\ 0 &1 &0 \\ 0 &0 &0 \end{pmatrix}+o_3 \begin{pmatrix} 0 &0 &0 \\ 0 &0 &0 \\ 0 &0 &1 \end{pmatrix}=\begin{pmatrix} o_1 &0 &0 \\ 0 &o_2 &0 \\ 0 &0 &o_3 \end{pmatrix}$

Each $o_i$ is a diagonal element of the operator, as well as an eigenvalue of the operator.

In other words, any operator can be expressed in the form of a diagonal matrix if it has the following properties:

1. Eigenvectors of the operator form a complete set, i.e. the eigenvectors span the vector space.
2. Eigenvectors of the operator are orthogonal or can be chosen to be orthogonal.

If the eigenvalues of $\hat{O}$ are real,

$\hat{O}^\dagger=\begin{pmatrix} o_1^* &0 &0 \\ 0 &o_2^* &0 \\ 0 &0 &o_3^* \end{pmatrix}=\begin{pmatrix} o_1 &0 &0 \\ 0 &o_2 &0 \\ 0 &0 &o_3 \end{pmatrix}=\hat{O}$

This implies that a Hermitian operator can also be expressed in the form of a diagonal matrix because the properties of a Hermitian matrix are:

1. Eigenvectors of the operator form a complete set, i.e. the eigenvectors span the vector space.
2. Eigenvectors of the operator are orthogonal or can be chosen to be orthogonal.
3. Eigenvalues of the operator are real.
4. $\hat{O}$ .

Spectral decomposition of an operator

Question

Answer

Question

Answer

Next article: matrix elements of an operator

Previous article: the uncertainty principle

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply