The matrix elements of an operator are the entries of the matrix representation of the operator.
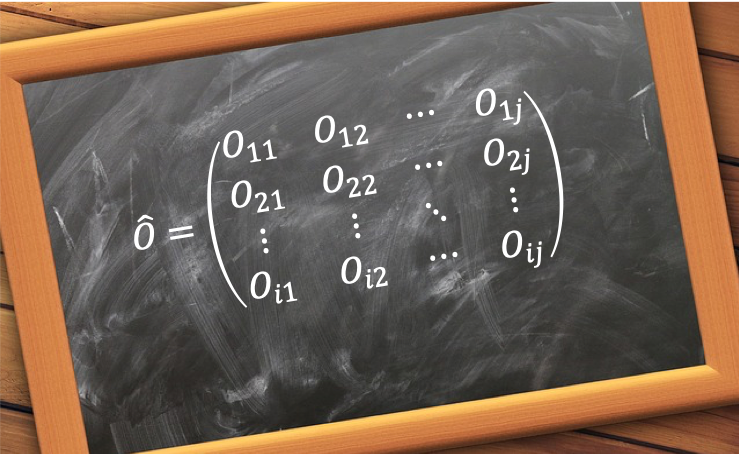
Consider a linear map from a vector space to the same vector space, i.e.
, where
and the orthonormal basis states
span
. The matrix representation of the equation is
where and
are the coefficients of the vectors
and
respectively.
The matrix elements of are given by
Since the orthonormal basis states span
, we have
. So,
Similarly, and so
Comparing eq33 with eq32a, . Therefore,
are the matrix elements of
with respect to the basis states of
.
