Bell’s inequality, developed by John Bell in 1964, is a non-equal relation (between two expressions) that is based on the ERP paradox. It provides a way to determine whether quantum theory or the EPR paradox is correct. Bell suggested a unique way of measuring the spins of two spin- particles, which are generated from the decay of a spin-0 particle at rest: the two particles are to be passed through two Stern-Gerlach devices, each oriented along one of three non-orthogonal coplanar axes, which are specified by the unit vectors
,
and
.
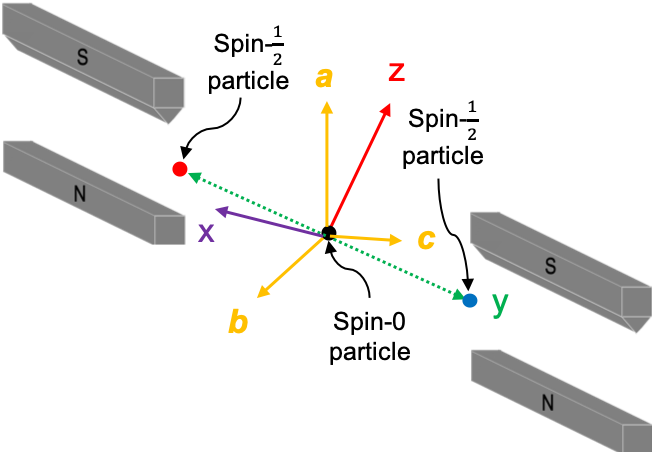
The average values of the product of the spins in units of (denoted by
,
, and
) are then calculated. As derived in an earlier article (see eq227), quantum mechanics expresses the average values as:
For the ERP paradox, let’s equate a spin-up measurement to +1 and a spin-down measurement to -1. The average value of the product of the measured spins, for example in the and
directions, is:
where
i) is a hidden variable.
ii) is the probability density that is a function of
, with
and
.
iii) is a function of the axis of measurement and
. It is associated with the measurement made by the first Stern-Gerlach device, and has output values of
.
iv) is a function of the axis of measurement and
. It is associated with the measurement made by the second Stern-Gerlach device, and has output values of
.
From experiments, we know that
Substitute eq230 in eq229
Similarly, and
. Therefore,
Since , we can rearrange the above equation to
Taking the absolute value on both sides of the above equation and using the relation

Question
Why is ?
Answer
For all , we have
. Therefore,
or simply
, where we have use the identity of
.
Since
Since and
, we can ignore the absolute value sign on RHS of the above equation:
Substitute and
into the above equation,
Eq232 is the Bell’s inequality, which is based on the ERP paradox.
To show that quantum mechanics is incompatible with Bell’s inequality, we let , i.e.
bisects
. From eq228,
Substitute eq233 and eq234 in eq232, we have , which is inconsistent with Bell’s inequality. Therefore, it is possible to experimentally measure the spins of the two particles at non-orthogonal angles to test the predictions of quantum theory versus the ERP paradox. In fact, the results of all experiments conducted at non-orthogonal angles were in agreement with quantum mechanics. This implies that all local hidden-variable hypotheses are invalid.