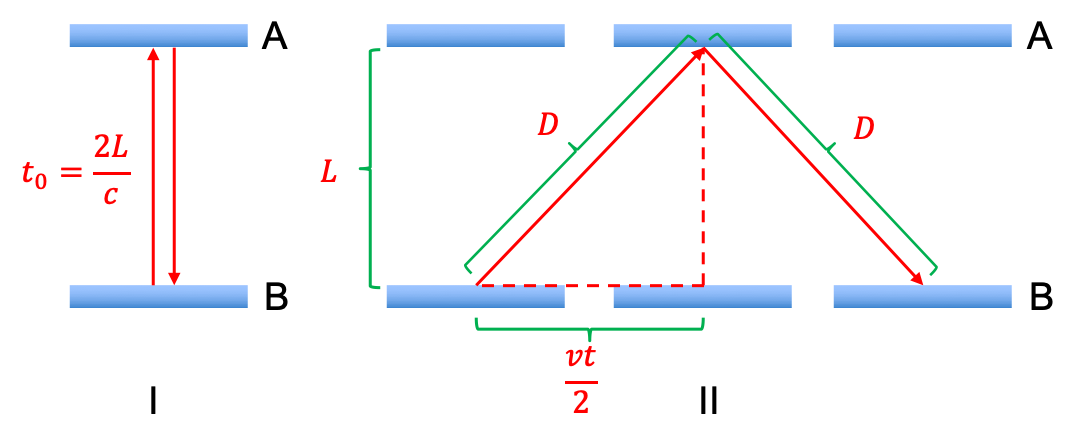
Time dilation is the difference in time measured by an observer who is moving relative to another observer. Consider two frames of reference, each with an observer and a clock, which consists of a photon bouncing between two mirrors A and B. If the frame of observer X is at rest, while the frame of observer Y is moving away from it, observer Y sees the photon of his clock travelling vertically between the mirrors (diagram I) and measures , where
is known as the proper time,
is the distance between the mirrors and
is the speed of light. Observer X, however, sees the same photon moving in a triangular path (as the observer X’s clock moves away from him) and measures
(diagram II), where
is the time recorded using his own clock.
Substituting , where
is the speed of the moving frame relative to the rest frame, and
in
, we have
where is called the Lorentz factor, which is useful in deriving the Thomas half.