Length contraction is the shortening of the length of a moving object, as compared to its proper length, which is measured by an observer at rest with respect to the object being measured. Consider a moving train with a clock, which consists of a photon bouncing horizontally between two mirrors A and B (see diagram below).
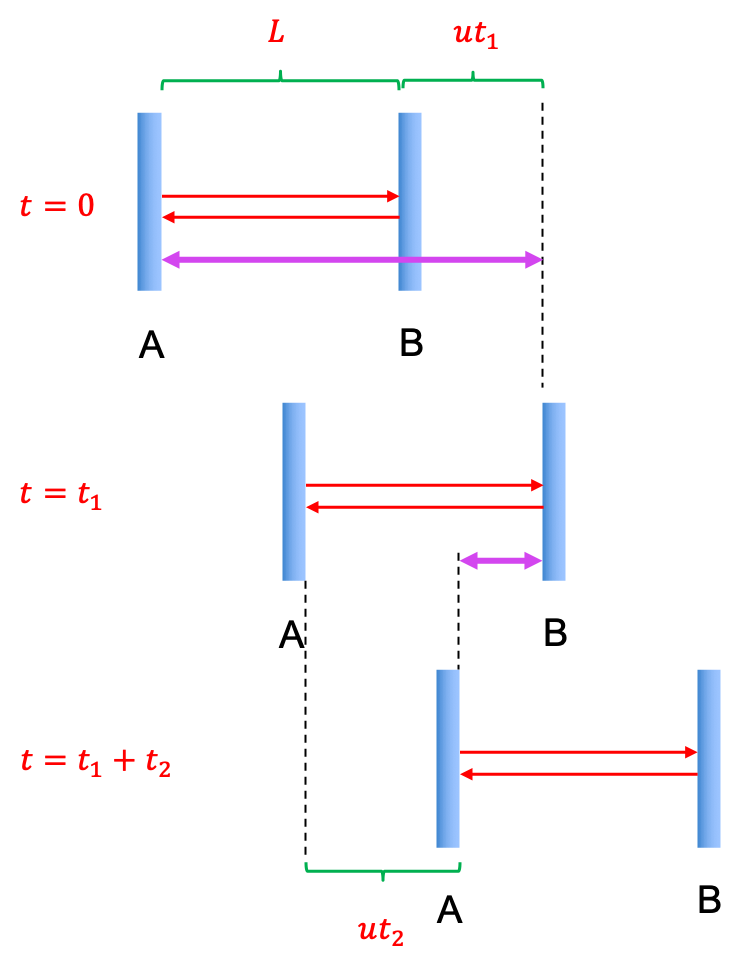
For observer X, who is at rest on a platform and seeing the passing train, the total distance travelled by the photon from A to B in (indicated by the top purple arrow) is
where is the speed of light,
is length of the clock according to X and
is the speed of the train.
When the photon returns from B to A in , A would have travelled a distance of
. Thus, the distance travelled by the returning photon from B to A (indicated by the bottom purple arrow) is
The total time taken is . Substitute eq250, where
, and eq251, where
, in
,
For observer Y, who is on the train, the total time measured by him is
, where
is called the proper length, which is the length measured by an observer who is at rest with respect to the object being measured. From eq249,
Equating eq251 with eq252,
where .