Koopmans’ theorem states that the energy to remove an electron from an orbital of an atom, whose state is described by a single Slater determinant, is approximately the negative value of the corresponding Hartree-Fock orbital energy. In other words, the theorem states that the negative value of the orbital energy of an atom is approximately equal to the ionisation energy IE for the k-th electron in the atom.
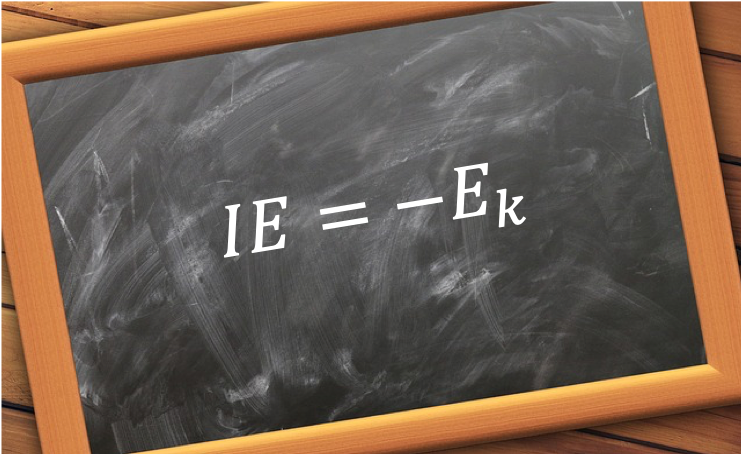
To prove the theorem, we begin with the ionisation process, which is generally expressed as
where is an atom, which is irradiated with a photon of energy
, and
is the corresponding ion with an electron
removed.
In terms of energies,
where is the state of the ion,
is the state of the atom and
is the kinetic energy of the expelled electron.
As ,
Substitute eq95 in eq143,

Question
Show that .
Answer
Let . Expanding the equation and eliminating common terms,
Since , we can add it to
, giving
Furthermore, and
. So,
Relabelling i to j for
Substitute eq145 in eq144,
Relabelling t with j and with
in eq109, we have
Multiplying the k-th equation in eq147 by and integrating over
, we have
Since
Substitute eq148 in eq146
Eq149 is known as Koopmans’ theorem.
Lastly, let’s study the relation between the relation between the orbital energy of an atom and the total energy E of the atom. From eq148,
Substitute eq94 in the above equation,

Question
Show that the alternative to eq150 is .
Answer
Adding to both sides of eq148 and summing throughout from
,
Since ,
