The Hartree-Fock-Roothaan method, an extension of the Hartree-Fock method, uses spin orbitals that are linear combinations of a set of basis wavefunctions .
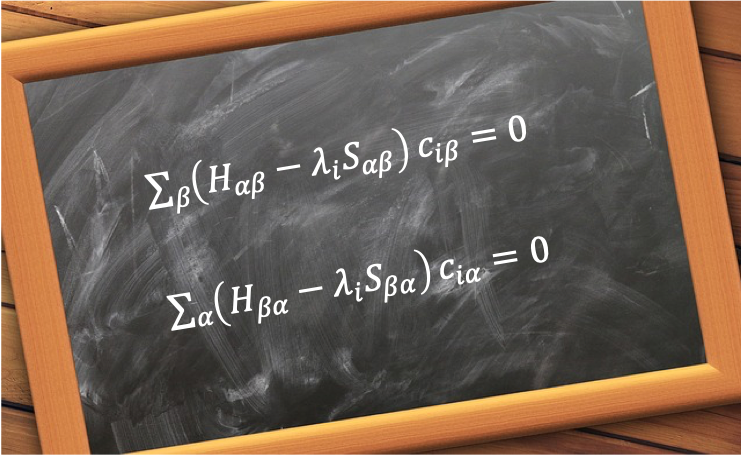
Unlike the Hartree-Fock method, in which the parameters of the wavefunctions are varied, the best basis wavefunctions
are chosen in the Hartree-Fock-Roothaan method and the coefficients
are instead varied in an iterative process to determine the state of the system.
To derive the Hartree-Fock-Roothaan equations, we begin by substituting and
in eq88, where we have relabelled
and
as
and
respectively, to give
where .
Next we substitute ,
,
and
in eq92 to give
where and
.
Substitute eq152 and eq153 in eq94,
The constraint for the Lagrange method is found by substituting and
in
to give:
where .
Therefore, the Lagrangian is:
where and
are the undetermined multipliers.
As shown in the derivation of the canonical Hartree-Fock equations, we can select a set of coefficients and
that diagonalises the Hermitian matrix with elements
. The Lagrangian becomes
The total differential of the Lagrangian is
where .
Eq155 has the same form as eq12. If we can find a set of values of that renders the dependent variable terms of
zero, we are left with the independent variable terms. Consequently, all the coefficients of
are equal to zero and they form a set of equations that can be solved simultaneously. To simplify eq155, substitute eq154 in it to give
The next step involves the following:
-
- Renaming the dummy indices of the 5th and 6th terms by swapping i and j,
and
,
and
, and the dummy coordinates
and
.
- Noting that
and
.
- Noting that
(see this article for explanation).
- Expanding each term of the equation and carrying out the partial differentiation.
- Renaming the dummy indices of the 5th and 6th terms by swapping i and j,
We have,
Switching the dummy labels ,
and
,
, and the dummy coordinates
and
for the 1st term on the RHS of the above equation,
where the 1st term of the above equation is the complex conjugate of the 2nd term.
Since all coefficients of and
are equal to zero, we have
where .
Similarly, the complex conjugate in eq156 gives:
Eq157 and eq158 are known as the Hartree-Fock-Roothaan equations.
Eq157 has non-trivial solutions if the determinant equals to zero. The computation process involves:
- Evaluating the integrals
and
either analytically or numerically using initial guess values of
, and with basis wavefunctions where the parameters are fixed.
- Substituting the evaluated integrals in the characteristic equation and solving for
, which is then used to obtain improved values of
for the next iteration.
- Repeating steps 1 and 2 with the improved values of
from the previous iteration until self-consistency is attained.