The root mean square speed of a gas is a statistical measure of the average speed of each particle in the gas.
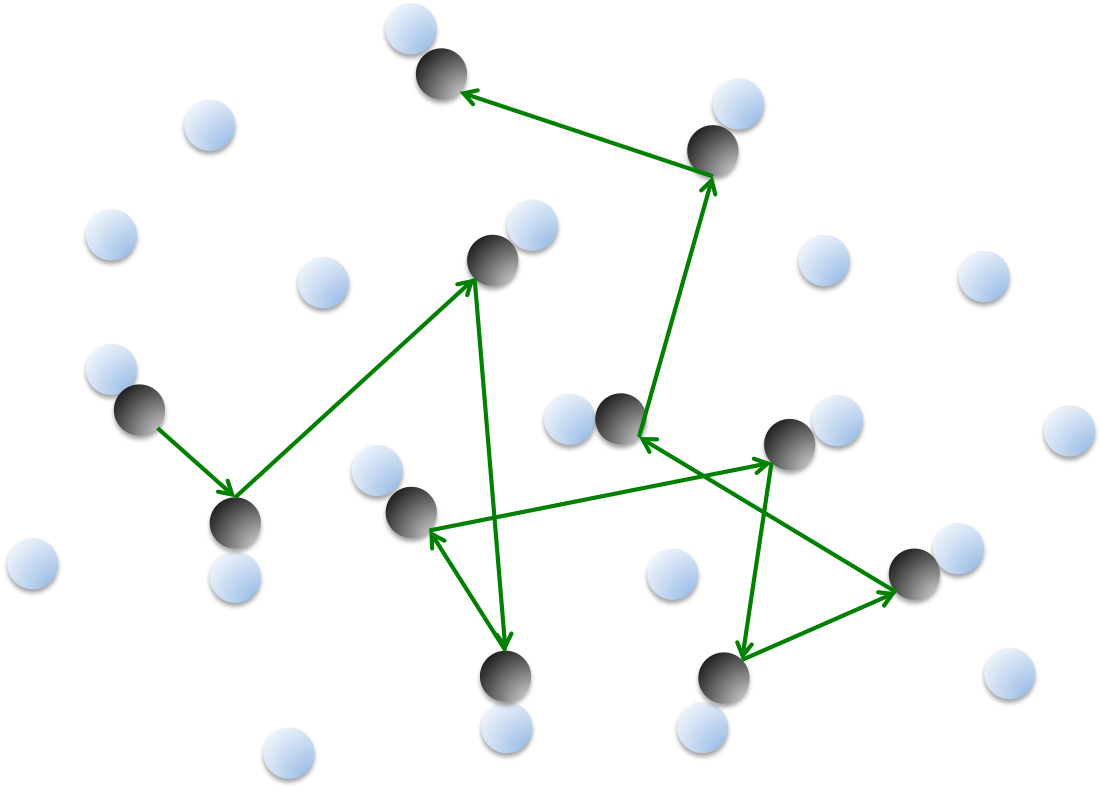
As mentioned in an earlier article, a gas in a container is made up of point masses that are moving randomly and colliding elastically with each other. The velocity of a gas particle is a vector with both magnitude and direction. With every elastic collision, the magnitude of a gas particle’s velocity is unchanged but its direction changes. The particles remain evenly distributed because the sum of the velocity vectors of all particles in the container at any time is zero (a non-zero net velocity implies that the particles are moving in a particular direction and are no longer in random motion).
We cannot determine the individual velocity of a gas particle and have to rely on an average value, which is zero as explained above. This poses a problem and we need to devise a different way to average the velocities of the particles. This new averaging method, which is described in the previous article, is called the root mean square speed and is given by
In the ideal case where the magnitudes of the velocities of all the particles are the same, is the same as taking the average of the absolute values of the velocities of the particles.