Carnot’s theorem states that no engine operating between two heat reservoirs of differing constant temperatures can be more efficient than a Carnot engine operating between the same reservoirs.
We have mentioned in an earlier article that an irreversible heat engine (real heat engine) is less efficient than a Carnot engine due to the occurrence of dissipative processes during the cycle, e.g. friction, with some of the work is converted to heat. Therefore, we just need to compare the efficiencies of reversible engines to prove Carnot’s theorem.

Consider a system of two reversible engines (see diagram above), where a reversible engine X is more efficient than the Carnot engine Y. This hypothetical greater efficiency for engine X can be brought about by a difference in design, a difference in working substance (e.g. different gas used) or both. From eq96 of a previous article,
In other words, for the same amount of thermal energy transferred to each engine (), the net work done by engine X is greater than that of engine Y,
.

Suppose we couple the engines, with engine Y running in reverse as a Carnot heat pump (see diagram above), where some amount of work from engine X () is used to run engine Y. Since
, the amount of heat transferred to engine Y from the cold reservoir is greater than the amount of heat deposited by engine X into the cold reservoir, i.e.
Engine Y is then adjusted to run at a rate such that it extracts heat from the cold reservoir at the same rate as engine X deposits heat to the cold reservoir (see diagram below).

For example, if engine Y extracts 1.5 times as much thermal energy per cycle from the cold reservoir as engine X deposits to the cold reservoir, engine Y is adjusted to run at two-third of its normal rate so that:
where is the factor of adjustment to engine Y.
Substitute eq107 in eq106, and noting that ,
From eq108, the work done by engine X is greater than the work required to run engine Y at the adjusted rate. If an equivalent work of from engine X is used to run engine Y, a net work of
is produced by the system. The amount of heat deposited in the hot reservoir by engine Y is
, which after substituting eq107 in it, becomes
, resulting in a net energy change of the hot reservoir of
. This means that the net energy extracted from the hot reservoir is completely used to produce a net work of
with zero net energy deposited at the cold reservoir, which violates the Kelvin-Planck statement of the second law of thermodynamics.
The assumption that the reversible engine X is more efficient than the Carnot engine Y is therefore false. Any reversible engine operating between two constant temperature reservoirs is either of equal efficiency or lower efficiency than a Carnot engine operating between the same reservoirs, i.e.
This dispels the notion that a reversible heat engine can be more efficient than a Carnot engine by a difference in design, a difference in working substance or both.

Next, we need to prove that any reversible engine has the same efficiency as a Carnot engine. We now run engine X in reverse and the Carnot engine Y in forward mode (see diagram above). If the Carnot engine Y is more efficient than the reversible engine X, we again violate the Kelvin-Planck statement. This means that
Eq109 and eq110 can only be reconciled if . Therefore, a Carnot engine has the same efficiency as any reversible heat engine working between the same constant temperature reservoirs.
Combining the two proofs, a Carnot engine, like any reversible heat engine operating between the same constant temperature reservoirs, is the most efficient heat engine.
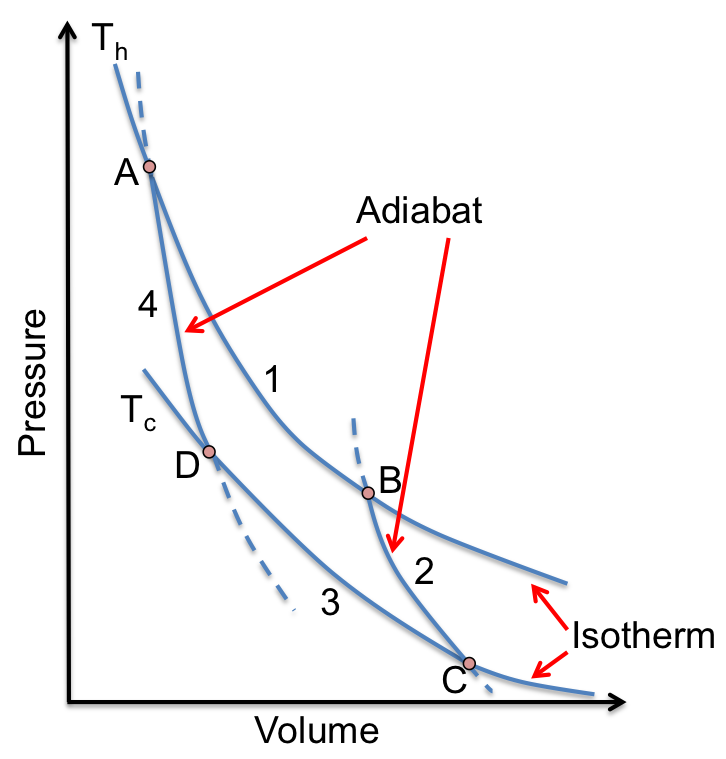
For a Carnot cycle with an ideal gas as the working substance (see diagram above), the work done during each of the processes is:
1) reversible isothermal expansion:
2) reversible adiabatic expansion:
3) reversible isothermal compression:
4) reversible adiabatic compression:
Even though the above work done equations pertain to an ideal gas, they are applicable to the calculation of the efficiencies of reversible engines with all types of working substances, as we have proven that the efficiency of a Carnot engine is independent of its working substance.
Net work done by the cycle is:
We have shown in an earlier article that . So,
According to the definition of a Carnot heat engine, is the transfer of heat from the constant temperature hot reservoir during step 1 of the Carnot cycle. This process is a reversible isothermal expansion with no change in internal energy of the system. So, from the first law of thermodynamics,
and
Substituting eq112 and eq113 in eq96,
Combining eq114 and eq97,

Question
What is the significance of eq114?
Answer
Prior to the derivation of eq114, temperatures are commonly measured on a mercury thermometer scale or a gas thermometer scale. In developing the mercury thermometer scale, the volume of mercury in a narrow column of a mercury thermometer is calibrated at the freezing point of water and the boiling point of water. The scale is then obtained by dividing the length of the mercury column into regular intervals between the two points. A similar procedure is employed to calibrate the volume of gas in a gas thermometer to form the gas thermometer scale. In each case, the calibrated temperature scale is dependent on the thermal expansion property of the working substance, which may not be completely linear. With eq114, a new temperature scale called the thermodynamic temperature scale is defined, where
Theoretically, the temperature of an object (cold reservoir) can be measured against a source (hot reservoir) at the triple point of water, 273.16 K by finding the efficiency of the engine used, which is independent of the property of the working substance as explained in the description of the Carnot engine. The triple point of water is chosen as a source temperature because it is a stable state that is easily reproduced. By making a temperature interval equal to a Kelvin, we have the thermodynamic temperature scale, which is equivalent to the absolute temperature scale of the ideal gas law. The equation above also suggests that the absolute zero of a system cannot be achieved. Otherwise,
, which violates the Kelvin-Planck statement of the second law of thermodynamics.
In practice, the thermodynamic temperature scale is based on the interpolation of a few easily reproduced temperature points, e.g. triple point of water (273.16 K), triple point of hydrogen (13.8033 K), triple point of oxygen (54.3584 K), etc., all of which can be accurately measured by sensitive instruments.
