Point group

A point group consists of geometric transformations known as symmetry operations, which preserve a single common point while transforming an object defined in a real vector space into physically indistinguishable replicas of itself.

Although an object undergoing a symmetry operation ends up looking the same after the transformation, the labelling of similar components of the object may change. In other words, to form a point group, all symmetry operations for an object must:

1. Send the object into physically indistinguishable copies of itself.
2. Combine with one another through binary operations such that the results are consistent with the 4 properties of a group.
3. Leave one point invariant.

Point groups are determined by considering symmetry operations for different objects, beginning with simple shapes and moving on to more complex ones. According to the three abovementioned requirements, we start by inspecting the chosen object visually and finding all the symmetry elements (not to be confused with group elements) and their associated symmetry operations. For example, the only symmetry elements for the object in figure I, which is made up of two equally spaced right-angled triangles on a circle, are the identity symmetry element $E$ and a 2-fold rotation axis $C_2$ . The corresponding symmetry operations are $\hat{E}$ and $\hat{C}_2$ .

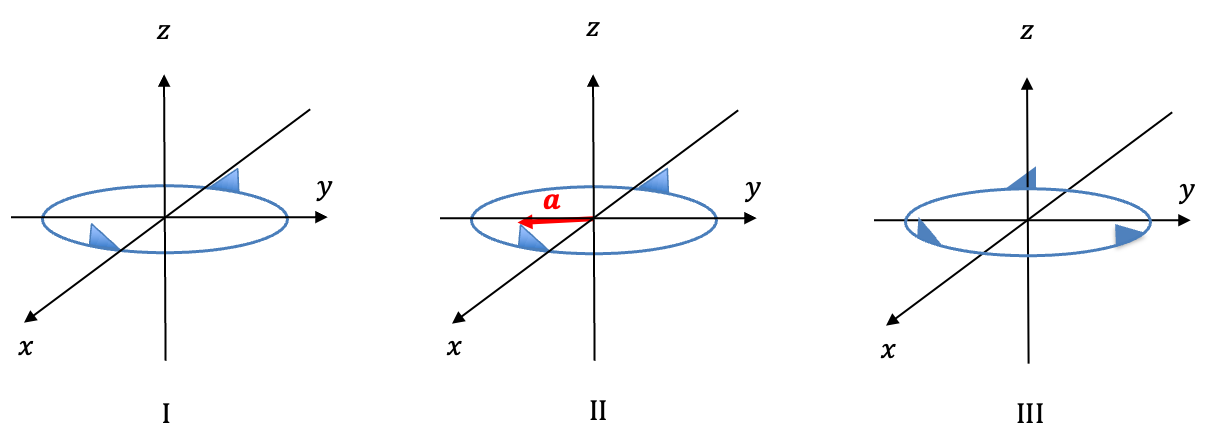
Next, we select a position vector $\boldsymbol{\mathit{a}}$ (see figure II) and perform the symmetry operations $\hat{E}$ and $\hat{C}_2$ consecutively on the position vector. The results, in relation to the transformation of the position vector, are summarised in the multiplication table i:

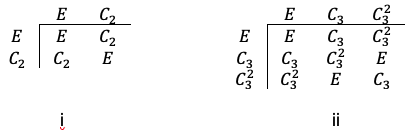
Note that we have omitted the carets – i.e. $\hat{E},\hat{C}_2\rightarrow E,C_2$ – for simplicity. From the table, we can easily verify all four properties of the group, e.g. the identity element is $E$ and the inverse of an element of the group is the element itself. Therefore, the set of symmetry operations $\{E,C_2\}$ for the object forms a point group of order 2 under the binary operation of multiplication. We call this group the $C_2$ point group. Similarly, the set of symmetry operations $\{E,C_3,C_3^2\}$ for the object in figure III forms the point group $C_3$ of order 3 (see multiplication table ii). In general, we have an infinite number of uniaxial point groups $C_n,n\in \mathbb{N}$ , each of which is called a cyclic group, whose elements are $E,C_n,C_n^2,\cdots ,C_n^{n-1}$ . For a cyclic group where $n$ is even, one of its elements is equivalent to the symmetry operation $C_2$ .

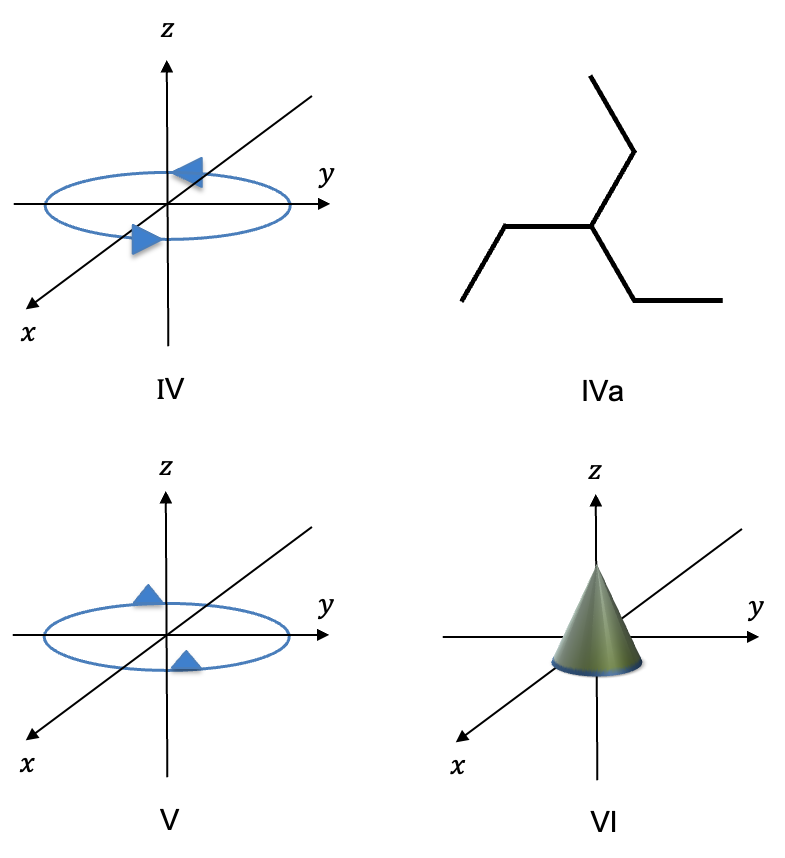
Let’s suppose the object in figure I have complete arrow heads (see figure IV). Other than $E$ and $C_2$ , the object has a plane of symmetry perpendicular to the axis of rotation (the horizontal plane is denoted by $\sigma_h$ ) and a centre of inversion $i$ at the origin. The set of symmetry operations $\{E,C_2,\sigma_h,i\}\equiv\{E,C_2,\sigma_h,S_2\}\equiv\{E,C_2,\sigma_h,\sigma_hC_2\}$ forms the Abelian point group $C_{2h}$ (see multiplication table iii). The object in figure IVa belongs to the $C_{3h}$ point group (see multiplication table iv) with the set of elements $\{E,C_3,C_3^2,\sigma_h,S_3,S_3^5\}\equiv\{E,C_3,C_3^2,\sigma_h,\sigma_hC_3,\sigma_hC_3^2\}$ , where $C_3^5=C_3^2$ . Similar to the $C_{n}$ point groups, if we apply the same logic to other related objects, we have an infinite number of $C_{nh}$ point groups, each with symmetry operations of $E,C_n,\cdots,C_n^{n-1},\sigma_h,\sigma_hC_n,\cdots,\sigma_hC_n^{n-1}$ if $n$ is even (one of the $\sigma_hC_n^{n-1}$ symmetry operations is equivalent to $i$ ) and $E,C_n,\cdots,C_n^{n-1},\sigma_h,\sigma_hC_n,\cdots,\sigma_hC_n^{2n-1}$ if $n$ is odd.

Question

Why aren’t $S_3^2,S_3^3,S_3^4$ and $S_3^6$ elements of the group $C_{3h}=\{E,C_3,C_3^2,\sigma_h,S_3,S_3^5\}$ ?

Answer

They are not unique elements, as they are equivalent to other ‘simpler’ elements of the group:

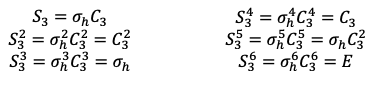
For an object that is made up of two equally spaced equilateral (or isosceles) triangles on a circle (see figure V above), we have the Abelian point group $C_{2v}$ , whose elements are the symmetry operations $E$ , $C_{2}$ , $\sigma_v$ and $\sigma_V'$ , where the symmetry elements for $\sigma_v$ and $\sigma_v'$ are the vertical planes: $xz$ -plane and $yz$ -plane respectively. The multiplication table for this point group is shown in table v above. As before, we have an infinite number of $C_{nv}$ point groups. The cone depicted in figure VI is an example of an object that belongs to the $C_{nv}$ point group, where $n=\infty$ , i.e. the $C_{n\infty}$ point group, with the set of symmetry operations: $\{E,C_{\infty}^+(\phi),C_2,C_{\infty}^-(\phi),\sigma_v(\varphi)\}$ .

Question

Are $C_1,C_{1h}$ and $C_{1v}$ point groups?

Answer

$C_1$ is a trivial point group whose sole element is the symmetry operation $E$ . An object of this group is considered to have no rotational symmetry.

$C_{1h}$ and $C_{1v}$ have the same set of symmetry operations: $\{E,\sigma\}$ . Since objects of both point groups have no rotational symmetry, the symbol for the reflection symmetry operation does not have a subscript. In fact, these point groups are so unique that they are collectively known as the point group $C_s$ (for Spiegel, the German word for mirror).

Another unique point group not mentioned above is $C_i$ , whose elements are the symmetry operations $E$ and $i$ . $C_1,C_{s}$ and $C_i$ are known as the non-axial point groups.

The next few related point groups are $D_n,D_{nh}$ and $D_{nd}$ (for dihedral). They are related in the sense that they have in common the elements $C_n$ and $nC_2'\perp C_{n}$ , which serve as identifiers in categorising molecules by point groups.

Example
Symbol	Object	Group elements	Notes
$D_2$		$E,C_2,C_2',C_2''$	The object is cyclohexane in its twisted boat form. A rhombic disphenoid (tetrahedron with scalene triangles as its faces) also belong to this point group.
$D_{2h}$		$E,C_2,C_2',\\C_2'',\sigma_{h},\sigma_v,\sigma_v',i$
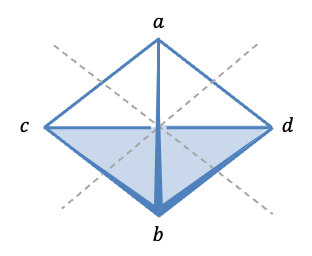$D_{2d}$		$E,C_2,C_2',\\C_2'',\sigma_{d},\sigma_d',\\S_4,S_4'$	The object is a tetragonal disphenoid (faces are isosceles triangles). $\sigma_d$ is a dihedral plane, i.e. a vertical plane that bisects the angle between two $C_{2}$ axes. 1) $C_{2}$ axis $\perp$ to screen and bisects $ab$ . 2) $2C_{2}\perp C_2$ axes, i) bisects $ac$ and $bd$ ; ii) bisects $ad$ and $bc$ . 3) $2\sigma_2d$ planes $\perp$ to screen, i) through $ab$ ; ii) though $cd$ .

The $D_1,D_{1h}$ and $D_{1d}$ point groups are identical to the $C_2,C_{2v}$ and $C_{2h}$ point groups respectively in non-standard orientation, i.e. the principal axis is along the $x$ -axis. A dumbbell has symmetry elements that are associated with the symmetry operations of

$D_{\infty h}=\{E,C_{\infty}^+(\phi),C_{\infty}^-(\phi),C_{\infty}^{+'}(\phi),C_{\infty}^{-'}(\phi),\sigma(\varphi),i,S_{\infty}^+(\phi),S_{\infty}^-(\phi)\}$

which is a special point group like $C_{\infty v}$ .

Next, we have the $S_n$ point group, which is in general associated with the symmetry operations $E,S_n,S_n^2,\cdots,S_n^{2n}$ . When $n=1$ , we have the point group $S_1=\{E,S_1\}=\{E,\sigma\}$ , which is the same as the point group $C_s$ . When $n=2$ , the point group $S_2=\{E,S_2\}=\{E,i\}$ is identical to the point group $C_i$ . For $n > 2$ , we need to analyse the point group $S_n$ with odd and even $n$ separately.

Consider an $S_n$ point group $G$ . When $n > 2$ is odd, the symmetry operation $S_n^n=\sigma_h^nC_n^n=\sigma_hE=\sigma_h$ . If $S_n\in G$ , then we have $S_n^n=S_n^{n-1}S_n\in G$ or $S_n^{n-1}\in G$ (according to the closure property of a group). Since $S_n^{n-1}S_n=\sigma_h$ , then $\sigma_h\in G$ . Moreover, $S_n=\sigma_hC_n$ , which implies that $C_n\in G$ . We can rewrite the symmetry operations of the $S_n$ point group ( $n > 2$ is odd) as

$E,C_n,\cdots,C_n^{n-1},\sigma_h,S_n,\cdots,S_n^{2n-1}=E,C_n,\cdots,C_n^{n-1},\sigma_h,\sigma_hC_n,\cdots,\sigma_hC_n^{2n-1}$

which is equivalent to the set of elements of the point group $C_{nh}$ . For example, the object in figure IVa belongs to the point group $S_3$ and hence to the point group $C_{3h}$ .

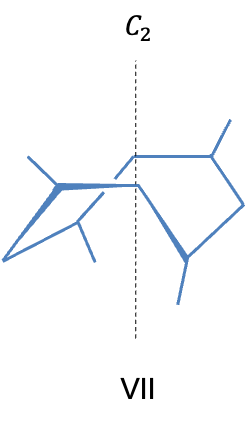
When $n > 2$ is even, the symmetry operation $S_n^n=\sigma_h^nC_n^n=EE=E$ . Since $S_n^{n},S_n\in G$ , we have $S_n^n=S_n^{n-1}S_n\in G$ or $S_n^{n-1}\in G$ . Similarly, $S_n^{n-1}=S_n^{n-2}S_n$ or $S_n^{n-2}\in G$ . This implies that $A=\{S_n^{n-1},S_n^{n-2},\cdots,S_n\}\in G$ . The elements of $A$ can be denoted by $S_n^k$ , where $k$ can be odd or even. If $k$ is even, then $S_n^k=C_n^k=C_{n/2}^{k/2}$ . For example, $S_6^2=C_6^2=C_3$ and $S_6^4=C_6^4=C_3^2$ . If $k$ is odd, then $S_n^k=\sigma_hC_n^k$ . We can therefore express the symmetry operations for the $S_n$ point group (when $n > 2$ is even) as $E,C_{n/2},\cdots,C_{n/2}^{k/2},\sigma_hC_n,\cdots,\sigma_hC_n^{n-1}$ . Figure VII depicts an object that belongs to the $S_4=\{E,C_2,S_4,S_4^3\}$ point group.

Taking into account the above characteristics of the $S_n$ point group, it is possible to relabel it as the $S_{2n}$ point group, where $n\in\mathbb{N}$ .

The rest of the point groups are the tetrahedral groups $T/T_d/T_h$ , the octahedral groups $O/O_h$ , the icosahedral groups $I/I_h$ and the special orthogonal group in 3-dimensions $SO(3)$ (also known as the full rotation group). The tetrahedral and octahedral groups are collectively called the cubic groups.

Symbol	Object	Group elements	Notes
$T$		$E,3C_2,4C_3,4C_3^2$	Each of the three $C_{2}$ axes passes perpendicularly through the centre of one of the three depicted faces, e.g. $abcd$ . Each of the four $C_{3}$ axes passes through one of four body diagonals, e.g. $cg$ .
$T_d$		$E,3C_2,4C_3,\\4C_3^2,3S_4,3S_4^3\\6\sigma_d$ or simply $E,3C_2,8C_3\\6S_4,6\sigma_d$	Same rotation axes as $T$ . Three $S_{4}$ axes (each with 2 symmetry operations: $S_{4},S_4^3$ ) coincident with the $C_{2}$ axes. Each of the six $\sigma_d$ passes through two diagonally opposite edges of the cube.
$T_h$		$E,3C_2,4C_3,\\4C_3^2,i,3\sigma_h,\\4S_6,4S_6^5$	Same rotation axes as $T$ . Four $S_{6}$ axes (each with 2 symmetry operations: $S_{6},S_6^5$ ) coincident with the $C_{3}$ axes. A centre of symmetry $i$ and three $\sigma_h$ : i) bisecting $ad$ and $eg$ , ii) bisecting $cd$ and $ef$ , iii) bisecting $de$ and $ag$ .
$O$		$E,3C_4,3C_4^3,\\4C_3,4C_3^2,\\6C_2',3C_2$ or simply $E,6C_4,8C_3,\\6C_2',3C_2$	Same as $T$ , but the $C_{2}$ axes are now $C_{4}$ axes (each with 3 symmetry operations: $C_{4},C_4^2=C_2,C_4^3$ ). Six $C_{2}'$ axes through mid-points of diagonal edges, e.g. $ab$ and $ef$ .
$O_h$		$E,6C_4,8C_3,\\6C_2',3C_2,\\i,3\sigma,8S_6,\\6S_4,6\sigma_d$	Same as $O$ , but includes centre of inversion $i$ , $S_{4}$ axes of $T_{d}$ and mirror planes of $T_{d}$ and $T_{h}$ .
$I$		$E,12C_5,12C_5^2,\\20C_3,15C_2$	The object is a snub dodecahedron with 92 faces (12 pentagons, 80 equilateral triangles), 150 edges and 60 vertices.
$I_h$		$E,12C_5,12C_5^2,\\20C_3,15C_2,i\\12S_{10},12S_{10}^3,\\20S_6,15\sigma$	The object is a truncated icosahedron with 32 faces (12 pentagons, 20 hexagons), 90 edges and 60 vertices. Same symmetry elements as $I$ with the addition of a centre of inversion, improper axes and mirror planes.
$SO(3)$		$E$ , all possible rotations	The object is a sphere with an infinite number of rotation axes, each with all possible values of $n$ .

Question

Why are $T_d$ and $O_h$ called tetrahedral point group and octahedral point group respectively?

Answer

A regular tetrahedron and a regular octahedron have all the same symmetry elements as those used to derive the $T_d$ point group and the $O_h$ point group respectively. A tetrahedron with reduced symmetry (e.g. with figure IVa attached to its faces) belongs to the $T$ point group. Similarly, an octahedron with attachments to its vertices belong to the $O$ point group.

Question

Answer

Question

Answer

Question

Answer

Next article: Molecular Point group

Previous article: Symmetry element and symmetry operation

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply