Schur’s first lemma states that a non-zero matrix that commutes with all matrices of an irreducible representation of a group is a multiple of the identity matrix.
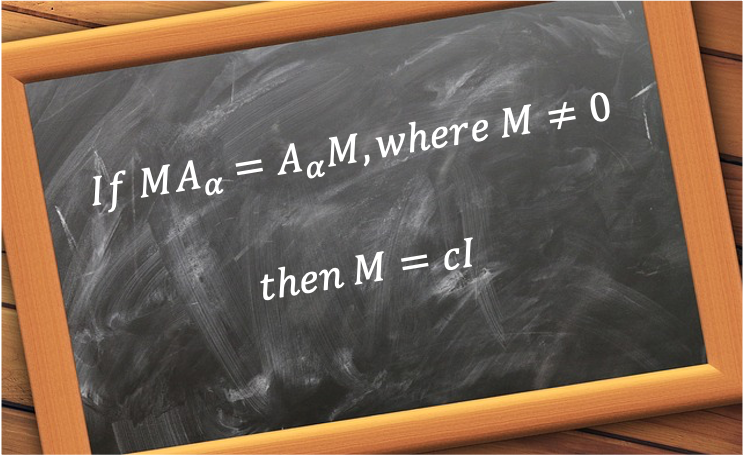
The proof of Schur’s first lemma involves the following steps:
-
- Consider a representation of a group
, i.e.
, where each element of
is an
matrix, which can be regarded as a unitary matrix
according to a previous article.
- Proof that a Hermitian matrix
that commutes with the irreducible representation element
, where
, is a constant multiple of the identity matrix.
- Infer from step 2 that any arbitrary non-zero matrix
that commutes with the irreducible representation element
is a multiple of the identity matrix.
- Consider a representation of a group
Step 1 is self-explanatory. For step 2, we begin with a Hermitian matrix that commutes with
:
Multiplying the above equation on the left and right by and
respectively,
Since
or
where .

Question
Show that is also a representation of
.
Answer
If is also a representation of
, its elements must multiply according to the multiplication table of
. Since
, we have
The third equality ensures that the closure property of is satisfied for
and hence
. In other words, the elements of
multiply according to the multiplication table of
.
As a Hermitian matrix can undergo a similarity transformation by a unitary matrix to give another Hermitian matrix which is diagonal, i.e.
, we have
Rewriting in terms of its matrix elements, we have
or
, which can be rearranged to
Consider the following cases for the above equation:
Case 1: All diagonal elements of are distinct, i.e.
if
.
We have for
, which means that all off-diagonal elements of
are zero. In other words,
is an element of a reducible representation that is a direct sum of
elements of one-dimensional matrix representations. Furthermore, the definition of a reducible representation implies that
is also an element of a reducible representation of
because
.
Case 2: All diagonal elements of are equal, i.e.
.
can be any finite number, and consequently
may be either an element of a reducible or an irreducible representation. However, the diagonal matrix
must be a multiple of the identity matrix if
.
Case 3: Some but not all diagonal elements of are equal.
Instead of considering all possible permutations of equal and unequal diagonal entries in , we rearrange the columns of
such that equal diagonal entries of
are in adjacent columns of
. This is always possible as the order of the columns of
corresponds to the order of the diagonal entries in
(see this article). Let’s suppose the first
diagonal entries are the same, while the rest are distinct, i.e.
. With reference to Case 1 and Case 2,
must be an element of a reducible representation with the block diagonal form:
For example, if in the following
matrix,
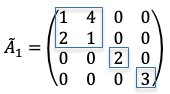
then can be any finite number, while all other off-diagonal elements are zero.
Combining all three cases, if is an irreducible representation, the diagonal matrix
must be a multiple of the identity matrix. Since
, where
is Hermitian, we have proven step 2.
For the last step, let’s consider an arbitrary non-zero matrix that commutes with
:
Since is unitary,
and so
, which when multiplied from the left and right by
gives
. This implies that if
commutes with
, then
also commutes with
.

Question
i) Show that if and
commutes with
, then any linear combination of
and
also commutes with
.
ii) Show that the linear combinations and
are Hermitian.
iii) Show that .
Answer
i)
ii)
iii) Substitute and
in
, we get
.
With reference to step 2, must be a constant multiple of the identity matrix and so must
. Therefore,
is also a constant multiple of the identity matrix. This concludes that proof of Schur’s first lemma, which together with Schur’s second lemma, is used to proof the great orthogonality theorem.