The normalisation constant ensures that the wavefunctions of the quantum harmonic oscillator are properly scaled, thereby maintaining the probabilistic interpretation of quantum states.

To derive the normalisation constant for the wavefunctions of the quantum harmonic oscillator, we begin with the multiplication of eq33 by and by itself (with a change of the dummy variable
to
and the dummy index
to
) to give
Integrating with respect to ,
Substituting the orthogonal relation when
in the above equation and simplifying, we have

Question
Show that .
Answer
Let and
. So,
with the limits unchanged. At the same time, let
, where we have changed the dummy variable
to
.
In polar coordinates, . For infinitesimal changes, the change in area
can be approximated as a rectangle with sides
and
(see diagram below), with
.
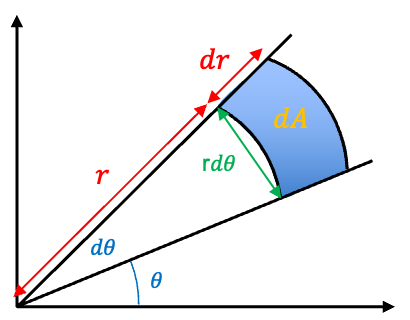
So,
Let
Using eq43 and the Maclaurin series expansion of , eq42 becomes
Expanding eq44 and comparing the coefficients of ,
In an earlier article, we have made a change of variable of in deriving the un-normalised wavefunction of the quantum harmonic oscillator. Since
is the variable representing position in the one-dimensional space that the oscillator is moving in, the normalisation of the wavefunction refers to an integral with respect to
, i.e.
Using , eq45 is equivalent to
Therefore,
The normalised wavefunction is then
or

Question
Show that is either an even function or an odd function.
Answer
An even function is defined as , while and odd function is when
. So,
is an even function. On the other hand,
is an even function if
is even and an odd function if
is odd. Since the product of two even functions is an even function, while the product of an odd function and an even function is an odd function,
is an even function when
is even and an odd function if
is odd.