The Taylor series is a way to express a function as an infinite sum of terms, each of which is derived from the function’s derivative value at a specific point 
.
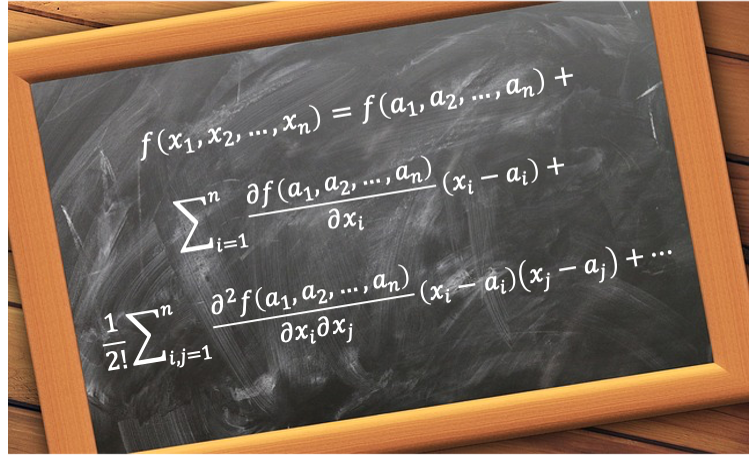
Consider the power series =c_0+c_1(x-a)+c_2(x-a)^2+\cdots+c_n(x-a)^n)
. We have =c_0)
, =c_1)
, =2c_2)
, =6c_3)
and so on. Therefore,
=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^n(a)}{n!}(x-a)^n\;\;\;\;\;\;\;\;32b)
Eq32b is called a Taylor series, which approximates a function in the neighbourhood of the point . When 
, the Taylor series is also known as a Maclaurin series:
=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^n(0)}{n!}x^n)
The input value 
of 
in eq32b represents points in the domain of that are near . In other words, we can express )
as ))
, where is a constant, 
is a variable, and 
represents a small change in that is scaled by . This alternate expression of is useful when dealing with multiple-variable functions.
For a multivariable function )
, the Taylor series about the point )
is
=f(a_1,a_2,\cdots,a_n)+\sum_{i=1}^n\frac{\partial f(a_1,a_2,\cdots,a_n)}{\partial x_i}(x_i-a_i)+\\\frac{1}{2!}\frac{\partial^2 f(a_1,a_2,\cdots,a_n)}{\partial x_i\partial x_j}(x_i-a_i)(x_j-a_j)+\cdots\;\;\;\;\;\;\;\;32c)
To derive eq32c, let )
and )
. Consider the function
=f(\hat{b}=\hat{a}+t(\hat{x}-\hat{a}))\;\;\;\;\;\;\;\;32d)
which implies that )
.
))
is a multivariable function, whose input is the vector )
, which varies with . In the domain of , 
is the vector representing a point where is expanded, and )
is a fixed vector that determines the direction of the displacement from the point . In other words, is not a variable of )
, but a parameter that we choose before plotting . The function is therefore a single variable function of , and its points are of the form ))
.
The Maclaurin series expansion of when 
is
=g(0)+\frac{g'(0)}{1!}+\frac{g''(0)}{2!}+\cdots\;\;\;\;\;\;\;\;32e)
According to the multivariable chain rule, }{dt}=\frac{\partial f(\hat{b})}{\partial x_1}\frac{dx_1}{dt}+\frac{\partial f(\hat{b})}{\partial x_2}\frac{dx_2}{dt}+\cdots+\frac{\partial f(\hat{b})}{\partial x_n}\frac{dx_n}{dt}=\nabla f(\hat{b})\cdot\frac{d\hat{x}}{dt}})
, where 
and 
. So,
=\nabla f(\hat{b})\cdot\frac{d\hat{x}}{dt}=\cdots=\sum_{i=1}^n\frac{\partial f(\hat{b})}{\partial x_i}(x_i-a_i)\;\;\;\;\;\;\;\;32f)
The second derivative =f''(\hat{b}))
is
=\frac{d^2f(\hat{b})}{dt^2}=\frac{d}{dt}\biggr\[\frac{\partial f(\hat{b})}{\partial x_1}\frac{dx_1}{dt}+\frac{\partial f(\hat{b})}{\partial x_2}\frac{dx_2}{dt}+\cdots+\frac{\partial f(\hat{b})}{\partial x_n}\frac{dx_n}{dt}\biggr\])
Using the multivariable chain rule again, we get
=\frac{d^2f(\hat{b})}{dt^2}=\sum_{i,j=1}^n\frac{\partial^2 f(\hat{b})}{\partial x_i\partial x_j}\frac{dx_i}{dt}\frac{dx_j}{dt}+\sum_{k=1}^n\frac{\partial f(\hat{b})}{\partial x_k}\frac{d^2x_k}{dt^2}\;\;\;\;\;\;\;\;32g)
With reference to eq32d, )
with components )
. It follows that 
, 
and 
. Eq32g becomes
=\frac{d^2f(\hat{b})}{dt^2}=\sum_{i,j=1}^n\frac{\partial^2 f(\hat{b})}{\partial x_i\partial x_j}(x_i-a_i)(x_j-a_j)\;\;\;\;\;\;\;\;32h)
Furthermore, when 
, we have 
. So, eq32f and eq32h become
=\sum_{i=1}^n\frac{\partial f(\hat{a})}{\partial x_i}(x_i-a_i)\;\;\;\;\;\;\;\;32i)
and
=\sum_{i,j=1}^n\frac{\partial^2 f(\hat{a})}{\partial x_i\partial x_j}(x_i-a_i)(x_j-a_j)\;\;\;\;\;\;\;\;32j)
respectively.
Substituting eq32i and eq32j in eq32e and noting that =f(\hat{a}))
and =f(\hat{x}))
, we have eq32c. Finally, the Maclaurin series of a multivariable function is
=\\\\\end{matrix}\begin{matrix}f(a_1=0,a_2=0,\cdots,a_n=0)+\\\\\sum_{i=1}^n\frac{\partial f(a_1=0,a_2=0,\cdots,a_n=0)}{\partial x_i}x_i+\\\\\frac{1}{2!}\frac{\partial^2 f(a_1=0,a_2=0,\cdots,a_n=0)}{\partial x_i\partial x_j}x_ix_j+\cdots\end{matrix}\;\;\;\;\;\;\;\;32k)
variables
,
, or
.