The quantum harmonic oscillator is a model for studying an atom that moves back and forth about an equilibrium point. The model’s central premise involves the use of the potential energy term of the classical harmonic oscillator to construct the Schrodinger equation for the harmonic oscillator:
which is equivalent to
where is the displacement of the mass from its equilibrium position.
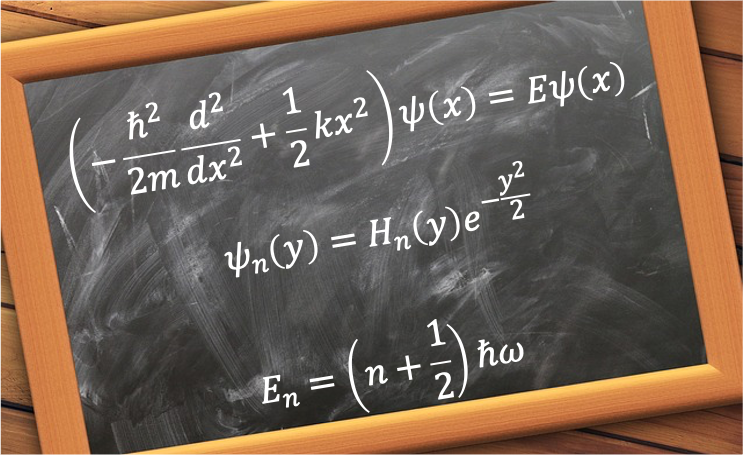

Question
Show that is equivalent to
.
Answer
The de Broglie relation is , where
. The derivative of the wavefunction
with respect to
is
This suggests that the operator is equivalent to
, and hence,
. Squaring the momentum operator
and dividing by
gives
.
Substituting in the above equation and rearranging, we have
The probability of locating an electron in the Hilbert space must be finite, i.e. . This implies that
vanishes as
. We call such a well-behaved wavefunction square-integrable. Hence, we need to study the asymptotic characteristics of eq5 to find possible solutions.
Let’s begin by simplifying the differential equation using a change of variable. Substituting and
in eq5, we have
Since is a constant,
as
, and eq6 approximates to
This suggests that the solution to eq6 could be a Gaussian function because is a solution to eq7. Let’s try
, where
is a function of
. Substituting
in eq6 and computing the derivatives, we have
Eq8 is known as the Hermite differential equation.

Question
Show that we can use a power series to solve eq8 around .
Answer
When , eq8 simplifies to
, where
. It can be easily verified that
and
are solutions to
. As the Taylor series for
and
are
and
, respectively, a power series is a solution to eq8 around
.
The above Q&A suggests that a possible solution to eq8 is a power series for a range of values of . Let
and substitute
and
in eq8 to give
Substituting and
in the above equation, we have
The above equation is only true for all values of if every coefficient for each power of
is zero. So,
, which rearranges to
Eq9 is a recurrence relation. If we know the value of , we can use the relation to find
. Similarly, if we know
, we can find
.
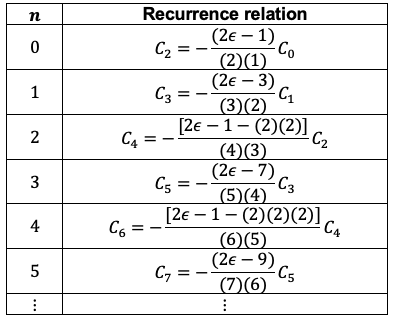
Comparing the recurrence relations for even-labelled coefficients,
Similarly, the recurrence relations for odd-labelled coefficients can be expressed as
Rewriting as a sum of two power series, one containing terms with even-labelled coefficients and the other with odd-labelled coefficients,
According to L’Hopital’s rule, appears to be a possible solution to eq7 because each of the terms in eq12 (simplified to
) approaches zero for large
:
where is a constant.
However, this does not guarantee that the series as a whole also converges because the sum of an infinite number of infinitesimal terms can still be infinite, as is the case for a harmonic series. To see how the two infinite series behave for large , we carry out the ratio test as follows:
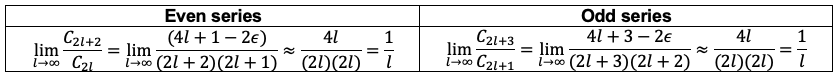
where we have set and
in eq9 for the even series and odd series respectively.
By comparison, the ratio test for the power series expansion of is also
. Therefore, both infinite series behave the same as
and diverge for large
. To ensure that
is square-integrable, we need to truncate either one of the series after some finite terms
and let all the coefficients of the other series be zero.

Question
Can we instead truncate both series of eq12 after some ?
Answer
Since the value of is arbitrary, the sum of two truncated series, each with finite terms, may still have an infinite number of terms. The only way to guarantee that
has finite terms is to truncate one of the series and let
, if the odd series is truncated, or
, if the even series is truncated, be zero.
To truncate either series, we let the numerator of eq9 be zero so that every successive term in the selected series is zero as well. This implies that
Let’s rewrite eq12 as
Since eq14 is the result of substituting in eq6, it is a solution to eq6.

Question
Show that .
Answer
We expand the even series in eq14 as follows:
Substituting eq9, where , in the above equation, we have
Substituting eq13 in the above equation gives the required expression.
Re-expanding the even series of eq14 using eq9 and eq13, we have
Comparing the coefficients of each even series in the above table, we have
where .
Similarly, the re-expansion of the odd series of eq14 using eq9 and eq13 gives
Comparing the coefficients of each odd series in the above table, we have
where .
The recurrence relation of eq9 that led to eq14 only defines the value of in terms of
. This implies that there are many solution sets depending on the value of
. The convention is to set the leading coefficients (i.e. the coefficients of
) of eq15a and eq15b, which are independent of each other, as
. Therefore,
and
Substituting eq16 and eq17 in eq14, we have , where
are the Hermite polynomials:
The first few Hermite polynomials, un-normalised eigenfunctions of eq6 and their corresponding eigenvalues are

When , we can express the Hermite polynomials for odd
as
Similarly, when , we can express the Hermite polynomials for even
as
Eq19 and eq20 are useful in proving the generating function for Hermite polynomials.
The table above also shows that the energy states of a quantum-mechanical harmonic oscillator are quantised:
with the ground state being non-zero. This energy is called the zero-point energy of the harmonic oscillator.

Question
Using the uncertainty principle, explain why the ground state of a quantum harmonic oscillator is non-zero.
Answer
If , then both the kinetic energy
and the potential energy
of the oscillator are zero.
implies that the momentum
is zero and
.
means that the atom is at the equilibrium position, where
. This would violate the uncertainty principle.
Since is a solution to eq8, we can rewrite eq8 as
To complete the prove that is a solution to eq6, we will derive the normalisation constant
of
and prove that the wavefunctions are orthogonal to one another in the next few articles.

Question
Do we have to change the variable back to
?
Answer
The Hermite polynomials are usually expressed in terms of because
looks more complicated:
Hermite polynomials
However, the normalisation constant is defined as an integral with respect to because
is the variable representing position in the one-dimensional space that the oscillator is moving in.