The harmonic oscillator

A harmonic oscillator comprises a particle that is subject to a restoring force proportional to the particle’s displacment $x$ from its equilibrium position.

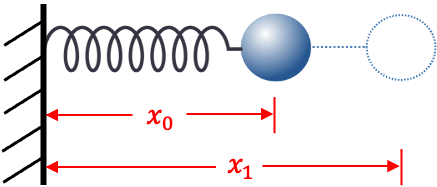
Consider a mass $m$ connected to a rigid support by a massless and frictionless spring (see above diagram). At equilibrium, the length of the spring is $x_0$ . Let’s assume that the only force $F$ acting on the mass is a restoring force that is directly proportional to the displacement of the mass (Hooke’s law):

$F=-kx\;\;\;\;\;\;\;\;1$

where $x=x_1-x_0$ is the displacement of the mass from its equilibrium position and $k$ is constant of proportionality called the force constant.

Question

Explain why $k$ is a measure of the stiffness of the spring.

Answer

For a particular value of $F$ , the stiffer the spring, the less the mass displaces. Since $k$ is inversely proportional to $x$ , it is a measure of the stiffness of the spring.

Substituting the equation for Newton’s 2^nd law of motion $F=ma$ in eq1, we have

$m\frac{d^2x}{dt^2}+kx=0\;\;\;\;\;\;\;\;2$

The solution to the above differential equation is $x=Asin\omega t$ , where $\omega=\sqrt{\frac{k}{m}}$ . As the displacement of the mass is defined by a wave equation, it is called a harmonic oscillator (‘harmonic’ originates from sound waves). The mass oscillates with amplitude $A$ and frequency $\frac{\omega}{2\pi}$ (see Q&A below), and the kinetic energy $E_k$ and potential energy $U$ of the system are

$E_k=\frac{1}{2}mv^2=\frac{1}{2}m\biggr$\frac{dx}{dt}\biggr$^2=\frac{1}{2}m$A\omega cos\omega t$^2$

$U=\frac{1}{2}kx^2=\frac{1}{2}k$Asin\omega t$^2\;\;\;\;\;\;\;\;3$

Question

Explain why the mass oscillates with a frequency of $\frac{\omega}{2\pi}$ and why the potential energy of the system is equal to $\frac{1}{2}kx^2$ ?

Answer

Since $x=Asin\omega t=Asin\biggr\[\omega\biggr$t+\frac{2\pi}{\omega}\biggr$\biggr\]$ , the function repeats itself after a time $\frac{2\pi}{\omega}$ . This implies that the period $T$ of the motion of the mass is $T=\frac{2\pi}{\omega}$ and that the oscillation frequency $\nu$ is $\nu=\frac{1}{T}=\frac{\omega}{2\pi}$ .

The force exerted by a person $F_p$ in lifting an object over a distance $x$ against gravity is $F_p=\frac{W}{\Delta x}$ , where $W$ is the work done by the person. $W$ must also be the amount of potential energy the object gains, i.e. $F_p=\frac{\Delta U}{\Delta x}$ . Furthermore, the force exerted by gravity $F$ is opposite to the force exerted by the person. So, $F=-\frac{\Delta U}{\Delta x}$ and for small changes, $F=-\frac{dU}{dx}$ . Since gravitational force and elastic spring force are both conservative forces (work done is path-independent, we substitute eq1 in $F=-\frac{dU}{dx}$ to give $dU=kxdx$ . Therefore, the potential energy of a harmonic oscillator is $U=k\int_0^xxdx=\frac{1}{2}kx^2$ .