Angular momentum is the rotational analogue of linear momentum . For a particle rotating in a plane at radius
about
(see diagram below), its velocity component
that is perpendicular to
is
where is the period (time taken to complete a revolution) and
is the angular velocity.
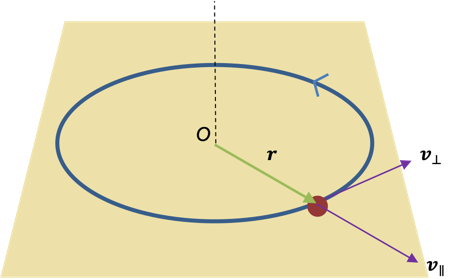
The rotational kinetic energy of the particle is
where is the moment of inertia.

Question
What is moment of inertia and why is it equal to ?
Answer
The moment of inertia is the rotational equivalent of a particle’s inertia in linear motion. For a particle in linear motion, its inertia is quantified by its mass. For a particle in rotational motion, its inertia is dependent on both its mass and the distribution of that mass relative to (i.e. dependent on
and
for a point mass). Since
, where
is the angular velocity of the rotating particle, we define
such that there is a correspondence between
and
, and between
and
.
Consequently, angular momentum , which is the rotational equivalent of linear momentum
, is defined as:
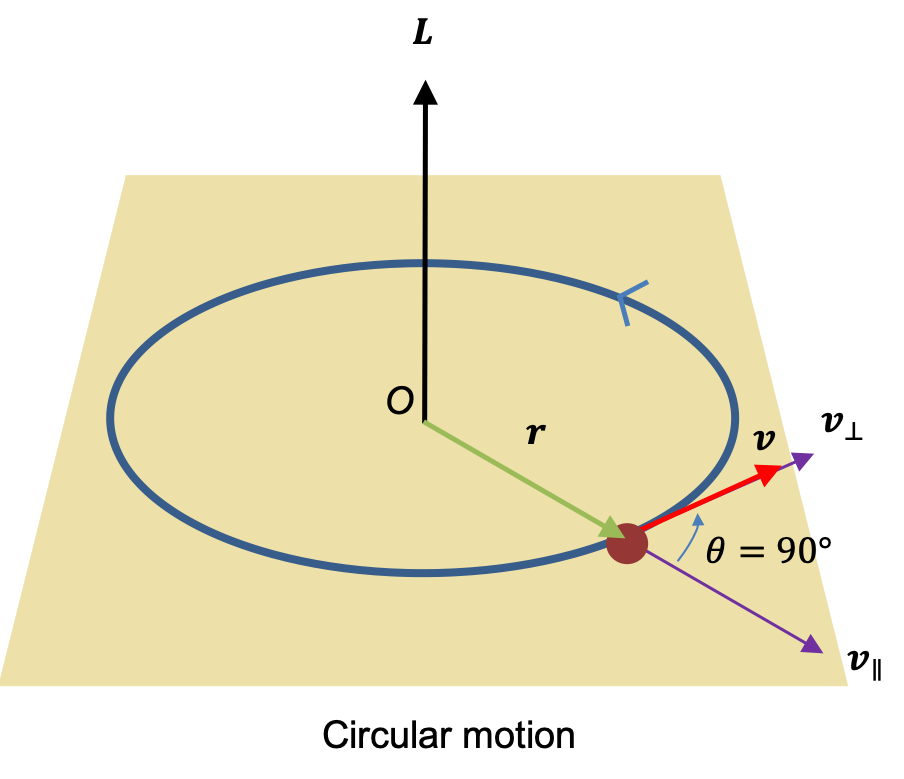
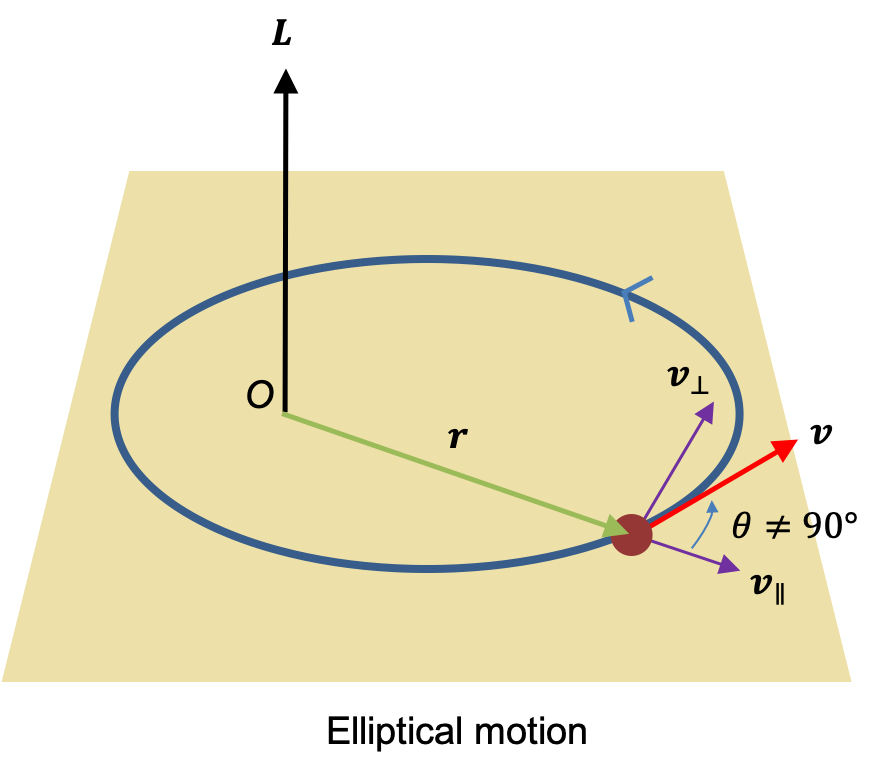
Since a particle’s orbit may be circular or non-circular (see diagram above), its angular momentum is generally expressed as:
or equivalently,
Therefore, angular momentum is a pseudo-vector with a direction indicated by the right-hand rule.
