Pauli matrices are matrix representations of the spin operators ,
and
.
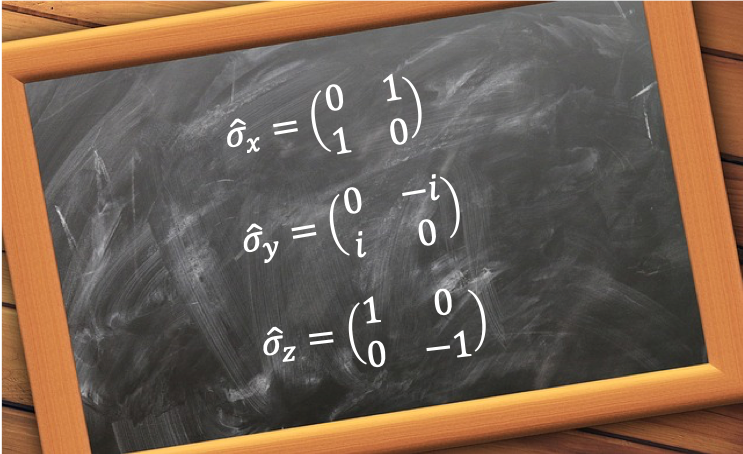
To derive the Pauli matrices, we let and
be basis vectors representing the electron spin eigenstates of
and
respectively, with the following assignments:
The general state of an electron can then be written as a linear combination of the two spin states:
where is the probability of finding the electron with the state
, and
is the probability of finding the electron with the state
, with
Having defined the two eigenstates, we can work out the corresponding matrix representation of using eq169 by letting
:
So,
Similarly, using eq168 for , we have
For and
, we make use of eq170 where
Since , we have
or
. Similarly,
. Using eq175 and eq176,
In an earlier article, when we constructed quantum orbital angular momentum component operators ,
and
, we replaced the position and linear momentum components of the classical angular momentum components
,
and
with their corresponding operators. We also suggested that we could have constructed an angular momentum operator using
, such that
, but for certain reasons chose to construct
instead. For electron spin, it is useful to construct the spin operator using that suggestion:
where , with
,
and
are called Pauli matrices. They represent observables and are Hermitian (the complex conjugate of each matrix returns the same matrix). Eq179 and eq180 are used to analyse the results of successive Stern-Gerlach experiments.

Question
Show that and
but
.
Answer
For , substitute in
and
and expand the expression. From eq102,
commutes with all components of
; and also all components of
because orbital angular momentum operators and spin angular momentum operators act on different vector spaces. Thus,
. Similarly, from eq165, eq166 and eq167,
commutes with all components of
and
and so
.
Now,
Substituting eq181 in and expanding the expression, we find, after some algebra, that
Similarly,