The Hamiltonian is invariant under a symmetry operation if its expression in different bases related by the symmetry operation is the same.
Our objective is to prove the above statement and that the Hamiltonian is invariant under a symmetry operation if it commutes with
.
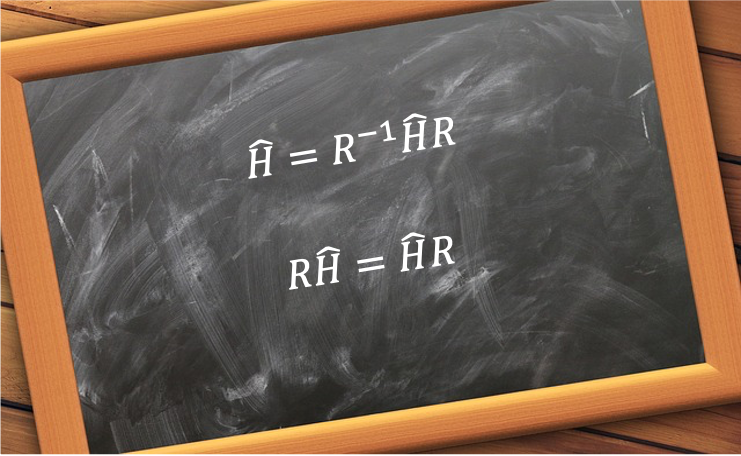
Let’s consider the non-relativistic multi-electron Hamiltonian :
where ,
and
.
The first term on the RHS of eq43 is the kinetic energy operator. To prove that it is invariant under any symmetry operation, we need to show that it is rotation-invariant and reflection-invariant. As mentioned in this article, we can analyse a symmetry operation in terms of the change of basis of a coordinate system. The following matrix equation expresses the change of basis of the operator by a rotation about the -axis:
where are components of a vector in the old basis, while
are components of the same vector in the new basis.
Since , we have
. That leaves us to show that
. From eq44,
Using the multivariable chain rule ,
Substituting eq47 in and
, we have
and
respectively. We then substitute these two equalities in eq48 to give:
Repeating the above logic for , we have
Adding eq49 and eq50 completes the proof.
The change of basis by a reflection, e.g. along the -plane, is given by
Since and
, we only need to show that
, which is achieved using the above logic for proving
.
The second and third terms on the RHS of eq43 (potential energy operator) are dependent on the electron-nuclear distance and the inter-electron distance
respectively. Since electron-nuclear distances and inter-electron distances do not change under symmetry operations,
and
.
Hence, is invariant to a change of basis related by
, and therefore, invariant under a symmetry operation
. Since
is invariant to a change of basis, it undergoes the following similarity transformation:
or equivalently,
Eq53 states that commutes with
, which is a consequence of
being invariant under the symmetry operation
.