A vector subspace is a subset of a vector space, and it is a vector space by itself.
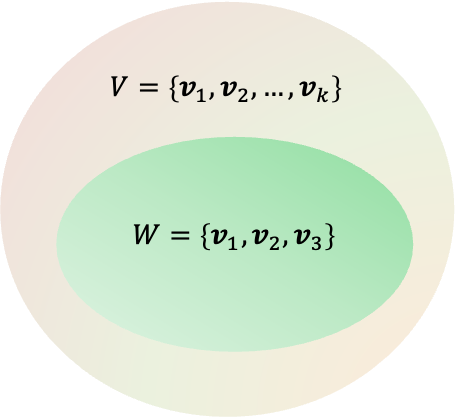
More formally, the vector subspace of the vector space
satisfies the following conditions:
1) Commutative and associative addition for all elements of the closed set.
2) Associativity and distributivity of scalar multiplication for all elements of the closed set
where and
are scalars.
3) Scalar multiplication identity.
4) Additive inverse.
5) Existence of null vector , such that
6) Closed under addition: the sum of any two or more vectors in is another vector in
.
7) Closed under scalar multiplication: the product of any vector in with a scalar is another vector in
.
For example, in the space, a plane through the origin is a subspace, as is a line through the origin. Hence,
and
are subspaces of
. The entire
space and the single point at the origin are also subspaces of the
space. This implies that a subspace contains a set of orthonormal basis vectors.
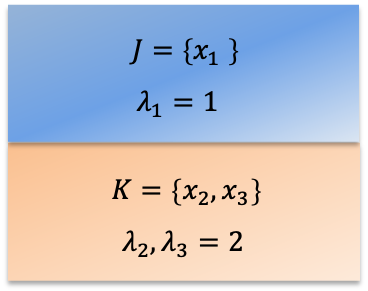
An eigenspace is the set of all eigenvectors associated with a particular eigenvalue. In other words, it is a vector subspace formed by eigenvectors corresponding to the same eigenvalue. Consider the eigenvalue equation , where
. If the eigenvalues of
,
and
are
,
and
respectively, then
and
are the eigenspaces of the operator
. Since an eigenspace is a vector subspace, it must contain a set of orthonormal basis vectors.

Question
Show that all orthonormal basis eigenvectors in an eigenspace
are linearly independent of one another.
Answer
A set of eigenvectors is linearly independent if the only solution to eq1 is when for all
. Taking the dot product of eq1 with
gives
which reduces to because
. Since
is arbitrary, we conclude that
and that the set
is linearly independent.