Buffer capacity of water

What is the formula describing the buffer capacity of water?

Consider a solution containing water and a strong base with the following equilibria:

$H_2O(l)\rightleftharpoons H^+(aq)+OH^-(aq)$

$NaOH(aq)\rightleftharpoons Na^+(aq)+OH^-(aq)$

With reference to the above equilibria, the sum of the number of moles of H⁺ and Na⁺ must equal to that of OH^–(see this article for details). As the volume of the solution is common to all ions,

$[H^+]+[Na^+]=[OH^-]\; \; \; \; \; \; \; \; (3)$

Substituting c_b = [Na⁺] and K_w= [H⁺][OH^–] in eq3 yields

$c_b=\frac{K_w}{[H^+]}-[H^+]$

$\frac{dc_b}{dpH}=\frac{dK_w[H^+]^{-1}}{dpH}-\frac{d[H^+]}{dpH}\; \; \; \; \; \; \; \; (4)$

Substituting eq1 and pH = –log[H⁺] in eq4 gives

$\beta_w=-\frac{dK_w[H^+]^{-1}}{dlog[H^+]}+\frac{d[H^+]}{dlog[H^+]}\; \; \; \; \; \; \; \; (4a)$

$\beta_w=ln10\left (\frac{K_w}{[H^+]}+[H^+] \right )\; \; \; \; \; \; \; \; (5)$

To determine the maximum or minimum buffer capacity of water, we take the derivative of eq5 with respect to [H⁺] to give:

$\frac{d\beta_w}{d[H^+]}=ln10\left (\frac{dK_w[H^+]^{-1}}{d[H^+]}+\frac{d[H^+]}{d[H^+]} \right )$

$\frac{d\beta_w}{d[H^+]}=ln10\left ( -\frac{K_w}{[H^+]^2}+1 \right )\; \; \; \; \; \; \; \; (6)$

Letting $\frac{d\beta_w}{d[H^+]}=0$ yields

$\frac{K_w}{[H^+]^2}=1$

Substituting K_w= [H⁺][OH^–] in the above equation results in

$[OH^-]=[H^+]$

This means that a stationary point for the function in eq5 occurs when [OH^–] = [H⁺] , i.e. at pH = 7. Let’s investigate the nature of this stationary point by differentiating eq6 again.

$\frac{d^{\, 2}\beta_w}{d[H^+]^2}=2ln10\frac{K_w}{[H^+]^3}$

Substituting K_w= [H⁺][OH^–] in the above equation, and noting that [OH^–] = [H⁺], gives

$\frac{d^{\, 2}\beta_w}{d[H^+]^2}=\frac{2ln10}{[H^+]}$

$\frac{d^{\, 2}\beta_w}{d[H^+]^2}> 0$

If we repeat the above steps and consider the case of the addition of a strong acid to water, we end up with the same conclusion. Hence, water has minimum buffer capacity at pH = 7.

The buffer capacity of water over the entire range of pH can be found by substituting [H⁺] = 10^-pHin eq5 to give

$\beta_w=ln10\left ( \frac{K_w}{10^{-pH}}+10^{-pH} \right )\; \; \; \; \; \; \; \; (6a)$

The plot of the above equation with β_was the vertical axis and pH as the horizontal axis is shown in the diagram below.

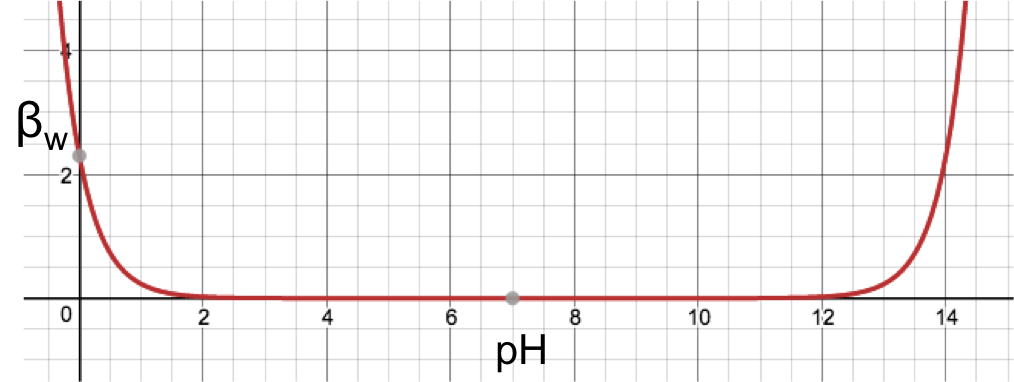
From the graph, the buffering capacity of water increases infinitesimally from a minimum of 0 at pH 7, to 0.023 at pH 2 on the left and pH 12 on the right, and then drastically to 2.303 at pH 0 on the left and pH 14 on the right. This means that water is only relatively effective as a buffer at extreme pH levels.

Buffer capacity of water

next article: Buffer capacity of an aqueous solution

Previous article: Buffer capacity

Content page of buffer solutions

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply