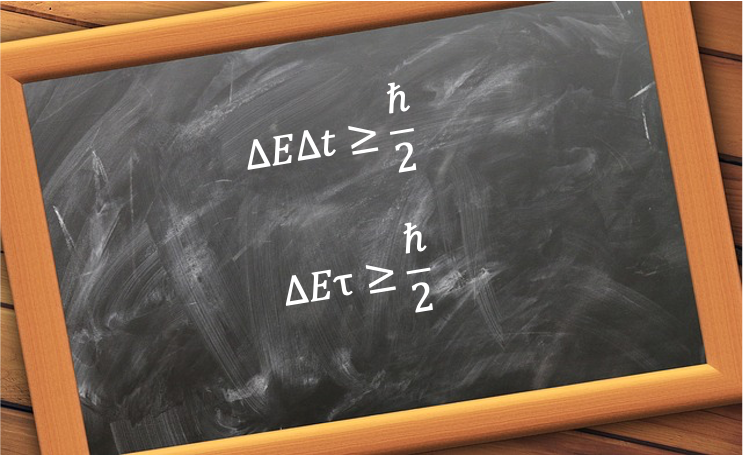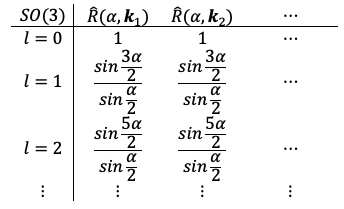An atomic clock is a highly precise timekeeping device that measures time based on the frequency of electromagnetic radiation emitted or absorbed during transitions between specific energy levels of atoms.

Traditional mechanical and even early electronic clocks are limited in accuracy because their timekeeping depends on macroscopic oscillations, such as pendulum swings or quartz vibrations, which are affected by temperature, friction, air pressure and other environmental factors. These variations cause conventional clocks to drift over time, making them unsuitable for applications that require extreme precision.
The idea of using atomic phenomena to measure time dates back to the 19th century. In his 1873 Treatise on Electricity and Magnetism, James Clerk Maxwell was among the first scientists to suggest that the oscillations of light waves could serve as a fundamental standard for time, laying the conceptual groundwork for the development of atomic clocks nearly a century later.
Building on Maxwell’s insight, modern atomic clocks achieve extraordinary precision by measuring the natural “ticks” of atoms rather than relying on macroscopic oscillations. One of the most widely used types is the caesium-133 atomic clock, which defines the second in the International System of Units (SI).
In the ground state, a caesium-133 atom has a single unpaired electron in its valence s-orbital, giving it the electronic configuration [Xe] 6s¹. For this electron, the orbital angular momentum is zero, and the spin angular momentum
is
, resulting in a total electronic angular momentum of
and the term symbol
. The nucleus, composed of protons and neutrons, has a collective nuclear spin of
.
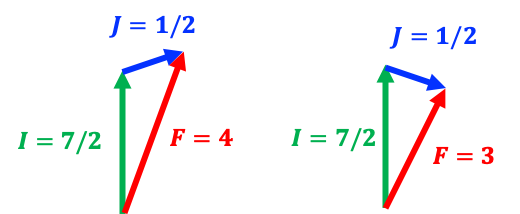
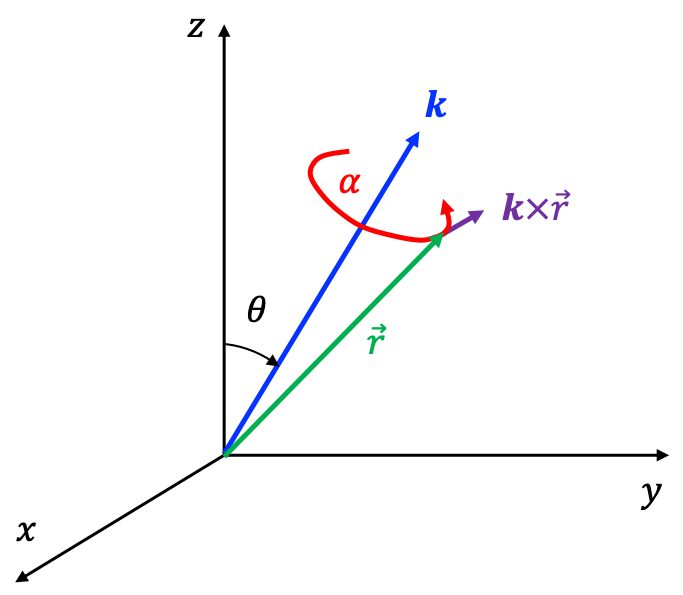
Both the electron and the nucleus generate magnetic fields associated with their respective magnetic dipole moments, and these fields interact with one another. This interaction, known as magnetic dipole coupling, causes the nuclear spin angular momentum to combine vectorially with the total electronic angular momentum (see diagram above), producing two total angular momentum states , where
and
is the projection of
onto the laboratory
-axis. The small energy difference
between these two states (see diagram below), known as the hyperfine splitting, forms the basis for the caesium atomic clock: by precisely measuring the frequency of radiation corresponding to transitions between these two states, the clock can maintain an exceptionally stable and accurate measure of time.
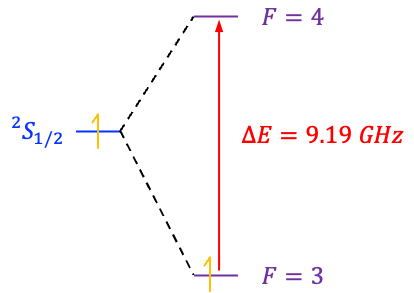

Question
Why is caesium-133 chosen as the standard for atomic clocks?
Answer
Caesium-133 is a stable isotope with a well-defined hyperfine splitting. Its hyperfine transition frequency of 9,192,631,770 Hz lies in the microwave region and is relatively insensitive to small variations in temperature, magnetic fields and electric fields compared to other atoms. This allows the transition to be generated and measured with exceptionally high precision in laboratory conditions.
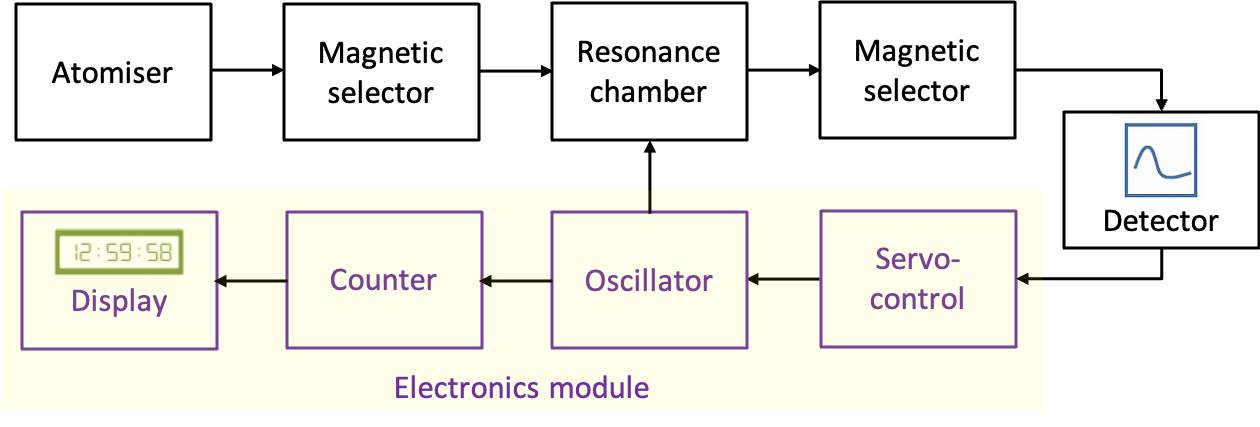
The main components of a caesium atomic clock include an atomiser, a magnetic state selector, a resonance chamber, a second magnetic selector, a detector and an electronics module (see diagram above). In the atomiser, an oven heats a small amount of metallic caesium, releasing atoms that pass through a narrow aperture to form a beam within a vacuum chamber. The oven temperature is carefully maintained at around 120°C to produce an adequate vapour pressure of caesium. At this temperature, the population ratio of atoms in the upper and lower hyperfine states follows the Boltzmann distribution:
Substituting ,
,
and
into the above equation gives:
Atoms in the lower hyperfine state are then selected and directed into the resonance chamber by a magnetic selector acting as a Stern-Gerlach device. Inside the chamber, the atoms are exposed to microwave radiation tuned near 9,192,631,770 Hz, corresponding to the transition between the two hyperfine levels. This frequency is generated by an electronic oscillator connected to both the resonance chamber and the detector in a feedback loop. When the microwave frequency exactly matches the transition, atoms in the lower state are driven to the upper state with maximum probability. After leaving the chamber, the beam passes through a second Stern–Gerlach device, which deflects unexcited atoms so that only those in the excited state reach the detector.
The detector measures the number of caesium atoms that arrive. Typically, this involves the atoms striking a hot surface, where they are ionised. The resulting ions or electrons are collected at an electrode, generating an electric current in the detector circuit that is proportional to the number of excited atoms reaching the detector. When the oscillator frequency is exactly equal to the transition frequency, the detector current reaches a maximum value, .
If temperature or other effects cause the oscillator frequency to drift from 9,192,631,770 Hz, the detector current decreases. A servo-control circuit detects this deviation and adjusts the oscillator frequency to restore the current to . This continuous feedback ensures that the oscillator remains precisely locked to the hyperfine transition frequency. The locked oscillator output is then sent to a counter circuit, which counts the oscillations and produces one output pulse each time exactly 9,192,631,770 cycles are completed — defining one second. These pulses drive a digital display, allowing the clock to show the precise time corresponding to the oscillations of the caesium atoms.
Modern caesium atomic clocks maintain accuracy to within a few billionths of a second per day and form the basis of Coordinated Universal Time (UTC), as well as global positioning and communication systems.

Question
Must the sample of caesium be replenished for the clock to run indefinitely?
Answer
Not often. In a caesium atomic clock, the atomisation process in the oven is extremely gentle. The oven warms a small quantity of metallic caesium, typically only a few grammes, to around 100–150 °C, producing a very low vapour pressure. This allows caesium atoms to slowly evaporate and form a steady atomic beam within the vacuum chamber. Only a tiny fraction of the atoms is emitted per second, perhaps 1012 to 1015 atoms per second. Compared to roughly 1021 atoms in one gramme of caesium (1 mole of caesium = 132.91 g), the sample is consumed at an exceedingly slow rate. The same small reservoir can therefore support continuous operation for many years, often 5 to 20 years or more, before the caesium becomes depleted or the oven performance degrades.
When that happens, the caesium source is simply replaced or refilled, and the clock continues operating as normal. In practice, the electronics or vacuum system usually require maintenance long before the caesium itself runs out. Thus, while the clock cannot run truly indefinitely, the atomisation process can indeed continue steadily for decades without needing frequent replenishment.