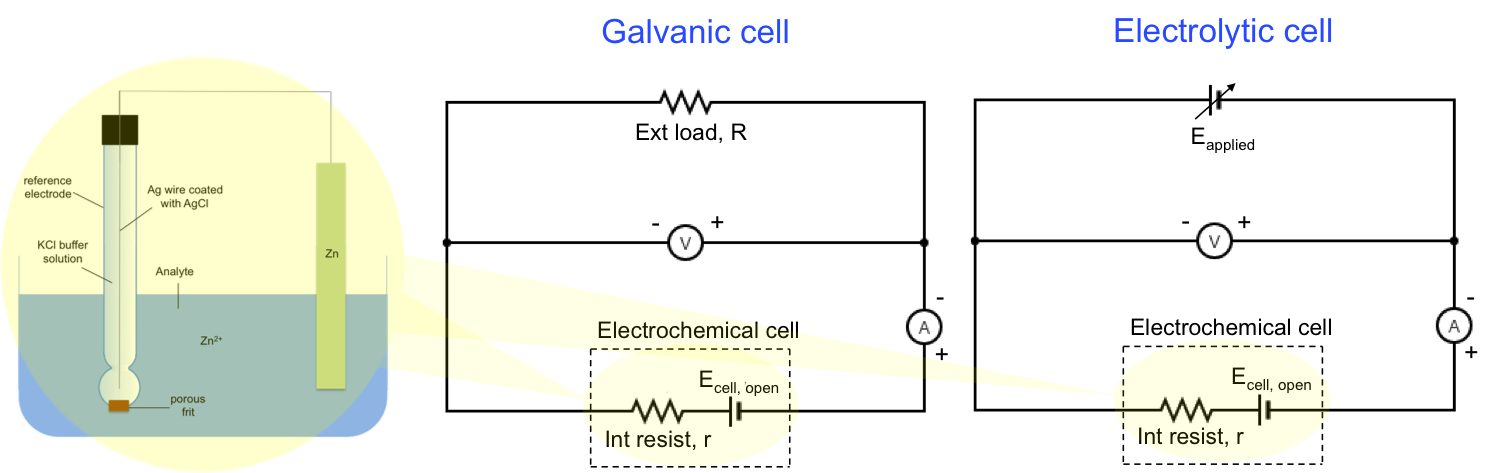
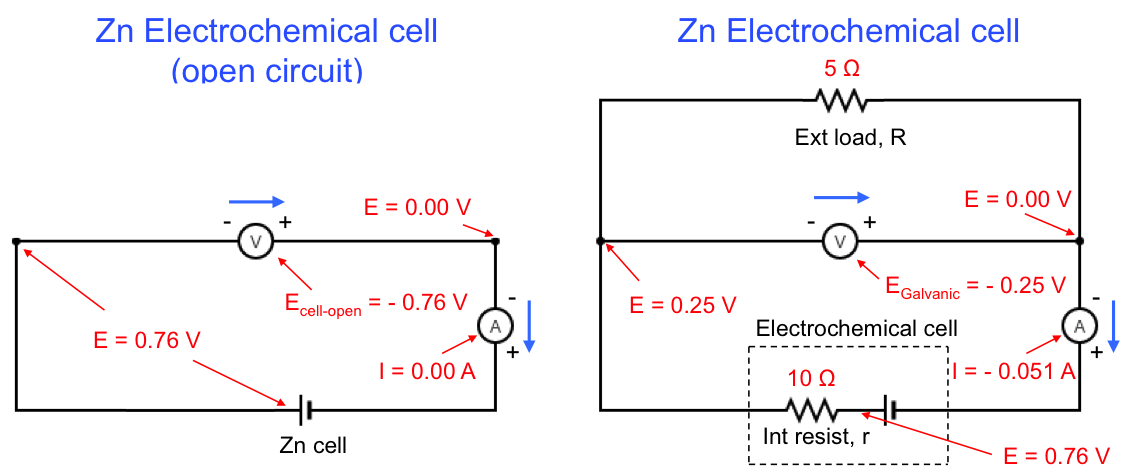
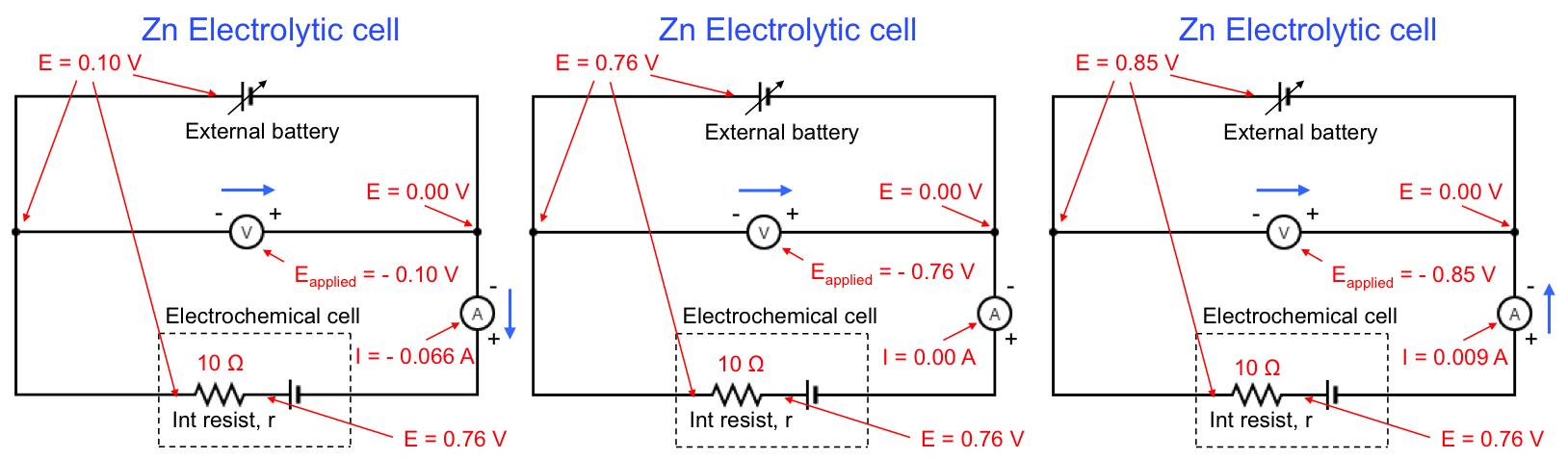
In 1887, Walther Nernst, a German chemist, developed the Nernst equation, which describes the relationship between an electrochemical reaction’s potential and its standard electrode potential under standard and non-standard conditions.
The derivation of the Nernst equation involves the following steps:
-
- Derive the formula for the reversible open circuit potential , Eo, of an electrochemical cell at constant temperature and pressure under standard conditions.
- Derive the expression for Eo in terms of chemical potentials of the reaction species at constant temperature and pressure.
- Derive a ‘correction factor’ for Eo in step2. This final expression, the Nernst equation, describes how the resultant Eo varies with activities of chemical species.
Step 1
From the definition of enthalpy, H = U + pV, we have
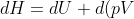\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;1)
Substitute the definition of the internal energy of a system undergoing reversible change, dU = dqrev + dwrev in eq1
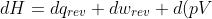\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;2)
Substitute the definition of the change in Gibbs energy of a system, dG = dH – d(TS) in eq2

At constant temperature and pressure, dT = dp = 0

Substitute the definition of the change in entropy of a system, dS = dqrev/T in eq3

Substitute the definition of total reversible work, wrev = wex + wadd, where wex is reversible expansion work and wadd is reversible additional work other than reversible expansion work, in eq4

Substitute the definition of the change in reversible expansion work, dwex = –pdV in eq5

Substitute the definition of the reversible electrical work between two points in an electric circuit, dwadd = –nFEdξ in eq6
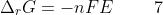
where n is the number of moles of electrons, F is the Faraday constant, E is the open circuit potential of the electrochemical cell and ΔrG = dG/dξ is the Gibbs energy of the electrochemical cell reaction.
When the open circuit potential of an electrochemical cell is measured at standard conditions (1 bar, 298K, 1M), we write eq7 as:

Step 2
The chemical potential of the j-th species, in a multi-component system is
_{T,p,n'}\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;9)
where n‘ is all n other than nj.
The total differential of the Gibbs energy of the system at constant temperature and pressure is
_{T,p,n'}dn_a+\left&space;(\frac{\partial&space;G}{\partial&space;n_b}&space;\right&space;)_{T,p,n'}dn_b+...\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;10)
Substituting eq9 in eq10

Eq11 can be expressed in another way by considering the reversible reaction

with the change in Gibbs energy at constant temperature and pressure of the system given by eq11. Next, let’s define

where vj is the stoichiometric number of the j-th species in the reversible reaction and dξ is the amount of substance that is being changed in the reaction.
ξ is called the extent of a reaction and has units of amount in moles. Note that the stoichiometric numbers for reactants are negative by convention and those for products are positive. Substituting eq12 in eq11
_{T,p}=&space;\sum_{j}\mu_jv_j\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;13)
Substitute the definition of the Gibbs energy of an electrochemical cell reaction, _{T,p}) , into eq13
, into eq13
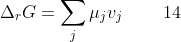
Substitute eq7 from Step1 in eq14

When the open circuit potential of an electrochemical cell is measured at standard conditions (1 bar, 298K, 1M), we write eq15 as:

Step 3
Firstly, let’s consider a system with a single pure substance. Substitute the definition of the change in Gibbs energy of a system, dG = dH – d(TS), in the change of enthalpy of the system dH = dU + d(pV)

The reversible change in internal energy of a pure substance (a system with a single pure substance only does expansion work) can be expressed as

Substitute the definitions of entropy, dS = dqrev/T, and expansion work, –pdV, in eq18

Substitute eq19 in eq17

At constant temperature, dT = 0 and eq20 becomes dG = Vdp. Integrating this new expression on both sides from 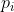 to
to  ,
,
=G\left&space;(&space;p_i&space;\right&space;)+nRTln\frac{p_f}{p_i})
Let pi = 1 bar = po (i.e. standard conditions) and pf = p

Secondly, we extend the above working to a multi-component system of ideal gases. Since G is an extensive property, we add the Gibbs energies of all components to give the total Gibbs energy of the system:
+\left&space;(&space;G_b^{\:&space;o}+n_bRTln\frac{p_b}{p_b^{\,&space;o}}&space;\right&space;)+...)
Let’s assume the reference pressures of the component gases are the same since they are all ideal gases, i.e. pao = pbo = po
+\left&space;(&space;n_aRTln\frac{p_a}{p^o}+n_bRTln\frac{p_b}{p^o}+...\right&space;))
)
For simplicity, let GTotal and GoTotal be G and Go respectively.
)
Taking the partial derivative of the above with respect to nj, at constant temperature, pressure and the amount of the other components, n‘, we have
![\left ( \frac{\partial G}{\partial n_j} \right )_{T,p,n'}=\left ( \frac{\partial G^{\, o}}{\partial n_j} \right )_{T,p,n'}+\left [ \frac{\partial \left ( n_aRTln\frac{p_a}{p^{\, o}}+ n_bRTln\frac{p_b}{p^{\, o}}+...\right )}{\partial n_j} \right ]_{T,p,n'}](https://latex.codecogs.com/gif.latex?\left&space;(&space;\frac{\partial&space;G}{\partial&space;n_j}&space;\right&space;)_{T,p,n'}=\left&space;(&space;\frac{\partial&space;G^{\,&space;o}}{\partial&space;n_j}&space;\right&space;)_{T,p,n'}+\left&space;[&space;\frac{\partial&space;\left&space;(&space;n_aRTln\frac{p_a}{p^{\,&space;o}}+&space;n_bRTln\frac{p_b}{p^{\,&space;o}}+...\right&space;)}{\partial&space;n_j}&space;\right&space;]_{T,p,n'})
For the last partial derivative of the above equation, only the j-th term survives.
_{T,p,n'}=\left&space;(&space;\frac{\partial&space;G^{\,&space;o}}{\partial&space;n_j}&space;\right&space;)_{T,p,n'}+RTln\frac{p_j}{p^{\,&space;o}}\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;21)
Substitute eq9 from Step 2 in eq21

Similarly, for a solute in a dilute solution satisfying Henry’s law, we can write

where cj and co are the j-th solute’s concentration and molar concentration respectively.
We can fine-tune eq22 and eq23 by replacing pj/po and cj/co with γj(pj/po) and γj(cj/co) where γj is a factor called the activity coefficient that can account for both ideal and non-ideal fluids (γ = 1 and γ < 1 for ideal and non-ideal fluids respectively). Next, we combine the modified equations into a single equation by letting aj = γj(pj/po) and aj = γj(cj/co), where aj is the activity of species j.

Substituting eq24 in eq15 from Step 2,
v_j=-\frac{1}{nF}\sum_{j}&space;\mu_j^{\,&space;o}v_j-\frac{RT}{nF}\sum_{j}v_jlna_j&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;25)
Substituting eq16 from Step 2 in eq25


where Q is the reaction quotient with Q =  .
.
Hence,  is the ‘correction factor’ for Eo, as the activities of reaction species vary. Eq26 is the Nernst equation.
is the ‘correction factor’ for Eo, as the activities of reaction species vary. Eq26 is the Nernst equation.
For an electrochemical equation of the form  , the Nernst equation can be written as:
, the Nernst equation can be written as:

Note that since Eo is by definition a reduction potential, the reference equation is always  and hence eq27.
and hence eq27.
in the above integral and working out some algebra yields