The third constitutive relation hypothesis states that the shear stress tensor is zero if the flow involves no shearing of the fluid-body.
A square matrix A is symmetric if aij = aji for all i and j, i.e. A = AT, e.g.
A square matrix is anti-symmetric (or skew symmetric) if aij = –aji for all i and j, i.e. –A = AT, e.g.
If aij = –aji , the diagonal components of the matrix must all be zero.
In general, we can write a square matrix in the following form:
where B = (A + AT)/2, C = (A – AT)/2 and AT is the transpose of A.
Using the transpose identity of (X + Y)T = XT+ YT (which can be verified by substituting any matrix with any components into the equality), we can show that B is symmetric (B = BT) and C is anti-symmetric (C = –CT).
This means that a square matrix can be decomposed into a symmetric and an anti-symmetric component. From the previous section, is a second-order tensor that can be represented by a 3×3 matrix. Therefore,
where is symmetric and
is anti-symmetric.
Substitute eq9 in eq8,
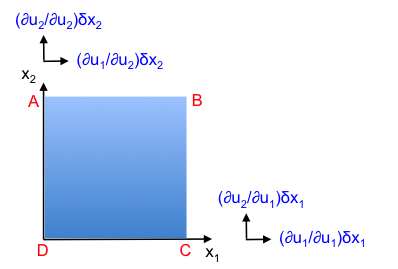
Consider a two-dimensional body of fluid ABCD as depicted in the above diagram. The term tends to shear the fluid. If we consider the rotation of the fluid in the clockwise direction, the term
tends to rotate the fluid. This means that
in eq9 can be non-zero even if the shear component
is zero, as the rotation component
is non-zero. However, hypothesis 3 states that the shear stress tensor τij in eq10 is zero if the flow involves no shearing of the fluid-body. To satisfy hypothesis 3, eq10 becomes:
βijkl , which is composed of eighty-one components, characterizes the properties of the fluid. Since is symmetric, and βijkl consists of scalar components, τij is also symmetric.