Eigenvalues of quantum orbital angular momentum operators

The eigenvalues of quantum orbital angular momentum operators are fundamental to understanding the quantisation of angular momentum in quantum mechanics, as they dictate the allowed energy levels and spatial distributions of particles in atomic and molecular systems.

As mentioned in an earlier article, if $\small \left [ \hat{L}^{2},\hat{L}_z \right ]=0$ , a common complete set of eigenfunctions can be selected for the two operators. Let $\small Y$ be the common set of normalised eigenfunctions with eigenvalues $\small b$ and $\small c$ for $\small \hat{L}^{2}$ and $\small \hat{L}_z$ respectively.

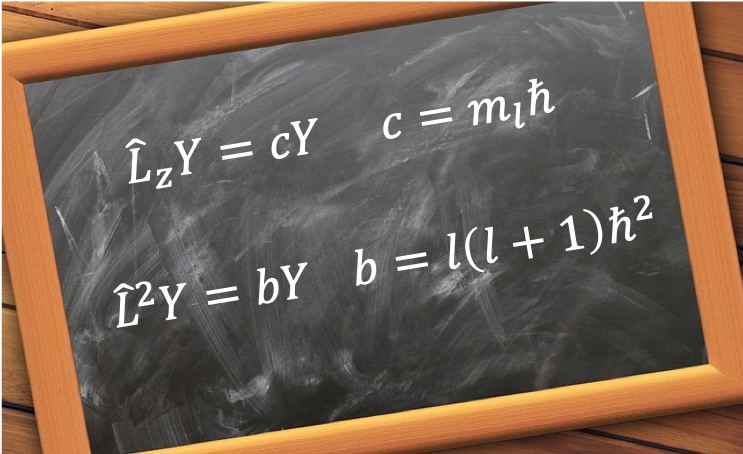
From eq75,

$\small \hat{L}^{2}-\hat{L}_z^{\; 2} =\hat{L}_x^{\; 2}+\hat{L}_y^{\; 2}$

Multiplying the above equation by $\small Y$ on the right, $\small Y^{*}$ on the left and integrating over all space, we have

$\small \langle L^{2}\rangle-\langle L_z^{\; 2}\rangle=\langle L_x^{\; 2}\rangle+\langle L_y^{\; 2}\rangle$

$\small b-c^{2}=\langle L_x^{\; 2}\rangle+\langle L_y^{\; 2}\rangle$

Even though $\small Y$ is not an eigenfunction of $\small \hat{L}_x^{\; 2}$ , we can still find the expectation value of $\small \hat{L}_x^{\; 2}$ , which is

$\small \langle L_x^{\; 2}\rangle=\int Y^{*}\hat{L}_x(\hat{L}_xY)d\tau=\int (\hat{L}_xY)(\hat{L}_xY)^{*}d\tau=\int \vert \hat{L}_xY\vert^{2}d\tau\geq 0$

Note that we have used the fact that $\small \hat{L}_x$ is Hermitian for the 2^nd equality (see eq37). Similarly, $\small \langle L_y^{\; 2}\rangle\geq 0$ . So,

$\small b-c^{2}\geq 0\; \; \; \; \; or\; \; \; \; \; -\sqrt{b}\leq c\leq \sqrt{b}$

Therefore, $\small c$ has an upper bound and a lower bound. Since the eigenvalues of $\small \hat{L}_z$ has an upper bound and a lower bound, from eq113 and eq114 we have

$\small \hat{L}_zY_{max}=c_{max}Y_{max}\; \; \; \; \; \; \; \; 122$

$\small \hat{L}_zY_{min}=c_{min}Y_{min}\; \; \; \; \; \; \; \; 123$

where $\small Y_{max}=\hat{L}_+^{\; k_{max}}Y$ , $\small c_{max}=c+k_{max}\hbar$ , $\small Y_{min}=\hat{L}_-^{\; k_{min}}Y$ and $\small c_{min}=c-k_{min}\hbar$ .

If we operate on eq122 with $\small \hat{L}_+$ , we supposedly have

$\small \hat{L}_z(\hat{L}_+Y_{max})=(c_{max}+\hbar)(\hat{L}_+Y_{max})$

However, the above equation contradicts the upper bound eigenvalue of $\small \hat{L}_z$ of $\small c_{max}$ . This implies that we must truncate the ladder beyond eq122. Since $\small c_{max}+\hbar\neq 0$ , we must have

$\small \hat{L}_+Y_{max}=0\; \; \; \; \; \; \; \; 124$

Using the same argument when operating on eq123 with $\small \hat{L}_-$ , we have

$\small \hat{L}_-Y_{min}=0 \; \; \; \; \; \; \; \; 125$

If we further operate on eq124 with $\small \hat{L}_-$ , we have

$\small \hat{L}_-\hat{L}_+Y_{max}=0$

Substitute eq116 in the above equation,

$\small (\hat{L}^{2}-\hat{L}_z^{\; 2}-\hbar\hat{L}_z)Y_{max}=0$

Using eq119 where $\small k=k_{max}$ , and eq122,

$\small (b-c_{max}^{\; \; \; \; \; \; 2}-\hbar c_{max})Y_{max}=0$

Since $\small Y_{max}\neq 0$

$\small b-c_{max}^{\; \; \; \; \; \; 2}-\hbar c_{max}=0 \; \; \; \; \; \; \; \; 126$

Similarly, operating on eq125 with $\small \hat{L}_+$ and using eq115, eq119 and eq123, we have

$\small b-c_{min}^{\; \; \; \; \; \; 2}+\hbar c_{min}=0 \; \; \; \; \; \; \; \; 127$

Subtracting eq127 from eq126, we have $\small (c_{max}+c_{min})(c_{min}-c_{max}-\hbar)=0$ . Since $\small c_{max}> c_{min}$ and $\small (c_{min}-c_{max}-\hbar)< 0$ , we have $\small c_{max}+c_{min}=0$ or

$\small c_{max}=-c_{min}\; \; \; \; \; \; \; \; 128$

As we know from eq122 and eq123, the value of $\small c_{max}-c_{min}$ of a particular system is dependent on the number of consecutive operations on $\small \hat{L}_zY$ by $\small \hat{L}_+$ or $\small \hat{L}_-$ , with each operation raising or lowering the eigenvalue of $\small \hat{L}_z$ by $\small \hbar$ . Therefore,

$\small c_{max}-c_{min}=0,\hbar,2\hbar,\cdots=2l\hbar\; \; \; \; \; \; \; \; 129$

where $\small l=0,\frac{1}{2},1,\frac{3}{2},\cdots$

Substituting eq128 in eq129, we have $\small c_{max}=l\hbar$ and $\small c_{min}=-l\hbar$ . Therefore, the eigenvalues of $\small \hat{L}_z$ are

$\small c=-l\hbar,-l\hbar+\hbar,-l\hbar+2\hbar,\cdots,l\hbar=-l\hbar,(-l+1)\hbar,(-l+2)\hbar,\cdots,l\hbar$

$\small c=m_l\hbar\; \; \; \; \; \; \; \; 130$

where $\small m_l=-l,-l+1,-l+2,\cdots,l$ .

Substituting $\small c_{min}=-l\hbar$ in eq127,

$\small b=l(l+1)\hbar^{2}\; \; \; \; \; \; \; \; 131$

where $\small l=0,\frac{1}{2},1,\frac{3}{2},\cdots$ .

As mentioned in the previous article, the raising and lowering operators also apply to the spin angular momentum $\small \boldsymbol{\mathit{S}}$ and the total angular momentum $\small \boldsymbol{\mathit{J}}$ . We would therefore expect the eigenvalues of $\small \hat{S}^{2}$ and $\small \hat{S}_z$ to be $\small s(s+1)\hbar^{2}$ and $\small m_s\hbar$ respectively, and the eigenvalues of $\small \hat{J}^{2}$ and $\small \hat{J}_z$ to be $\small j(j+1)\hbar^{2}$ and $\small m_j\hbar$ respectively. However, the quantum numbers $\small l$ and $\small m_l$ for the orbital angular momentum $\small \boldsymbol{\mathit{L}}$ , but not the quantum numbers for $\small \boldsymbol{\mathit{S}}$ and $\small \boldsymbol{\mathit{J}}$ , are restricted to integers. Therefore,

$\small \boldsymbol{\mathit{L}}$	$\small m_l\in \mathbb{Z}$	$\small l\in \mathbb{Z}$
$\small \boldsymbol{\mathit{S}}$	$\small m_s=-s,-s+1,-s+2,\cdots,s$	$\small s=0,\frac{1}{2},1,\frac{3}{2},\cdots$
$\small \boldsymbol{\mathit{J}}$	$\small m_j=-j,-j+1,-j+2,\cdots,j$	$\small j=0,\frac{1}{2},1,\frac{3}{2},\cdots$

Question

Why are the quantum numbers for $\small \boldsymbol{\mathit{L}}$ restricted to integers?

Answer

The eigenvalue equation for $\small \hat{L}_z$ (see eq95) is:

$\small \frac{\hbar}{i}\frac{\partial}{\partial\phi}\psi=m_l\hbar\psi$

where $\small \psi=Ae^{im_l\phi}$ .

Since $\small \psi$ must be single-valued,

$\small Ae^{im_l\phi}=Ae^{im_l(\phi+2\pi)}$

$\small e^{im_l2\pi}=1$

$\small cosm_l2\pi + isinm_l2\pi=1$

The solution to the above equation is $\small m_l\in \mathbb{Z}$ . Furthermore, $\small l$ is also an integer because $\small m_l=-l,-l+1,-l+2,\cdots,l$ . In other words, there are $2l+1$ values of $m_l$ for a given value of $l$ .

We would arrive at the same results (eq130 and eq131) if we have chosen $\small \hat{L}_x$ or $\small \hat{L}_y$ instead of $\small \hat{L}_z$ . The significance of eq130 and eq131 is that we can simultaneously assign eigenvalues of $\small \hat{L}^{2}$ and $\small \hat{L}_z$ (or $\small \hat{L}^{2}$ and $\small \hat{L}_x$ or $\small \hat{L}^{2}$ and $\small \hat{L}_y$ ) if the 2 operators commute. This, together with the fact that any pair of component angular momentum operators does not commute, implies that we cannot simultaneously specify eigenvalues of $\small \hat{L}^{2}$ and more than one component angular momentum operators.